《2025年文轩图书假期生活指导暑八年级数学通用版》

19. 如图,已知正方形$ABCD的边长为5$,点$E$,$F分别在AD$,$DC$上,$AE = DF = 2$,$BE与AF相交于点G$,点$H为线段BF$的中点,连接$GH$,求$GH$的长。

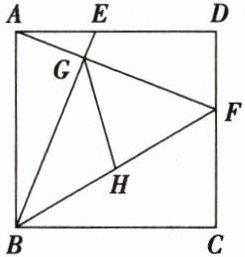
解: ∵ 四边形 ABCD 是正方形,
∴ ∠BAE = ∠D = ∠C = 90°, AB = AD = BC = CD = 5,
在 △ABE 和 △DAF 中,
{ AB = AD,
∠BAE = ∠D,
AE = DF
}
∴ △ABE ≌ △DAF(SAS),
∴ ∠ABE = ∠DAF,
在 Rt△ABE 中, ∠BAE = 90°,
∴ ∠ABE + ∠BEA = 90°,
∴ ∠DAF + ∠BEA = 90°,
在 △AEG 中, ∠AGE + ∠DAF + ∠BEA = 180°,
∴ ∠AGE = 180° - (∠DAF + ∠BEA) = 180° - 90° = 90°,
∴ 由对顶角性质可得: ∠AGE = ∠BGF = 90°,
∵ 在 Rt△BFG 中, 点 H 是 BF 的中点,
∴ GH = 1/2 BF,
∵ CF + DF = CD, DF = 2, CD = 5,
∴ CF = CD - DF = 5 - 2 = 3,
∴ 在 Rt△BCF 中,
由勾股定理得 BF = √(CF² + BC²) = √(3² + 5²) = √(9 + 25) = √34,
∴ GH = 1/2 BF = √34/2.

答案： 19. 解:
∵ 四边形 ABCD 是正方形,
∴ ∠BAE = ∠D = ∠C = 90°, AB = AD = BC = CD = 5,
在 △ABE 和 △DAF 中,
{ AB = AD,
∠BAE = ∠D,
AE = DF
}
∴ △ABE ≌ △DAF(SAS),
∴ ∠ABE = ∠DAF,
在 Rt△ABE 中, ∠BAE = 90°,
∴ ∠ABE + ∠BEA = 90°,
∴ ∠DAF + ∠BEA = 90°,
在 △AEG 中, ∠AGE + ∠DAF + ∠BEA = 180°,
∴ ∠AGE = 180° - (∠DAF + ∠BEA) = 180° - 90° = 90°,
∴ 由对顶角性质可得: ∠AGE = ∠BGF = 90°,
∵ 在 Rt△BFG 中, 点 H 是 BF 的中点,
∴ GH = 1/2 BF,
∵ CF + DF = CD, DF = 2, CD = 5,
∴ CF = CD - DF = 5 - 2 = 3,
∴ 在 Rt△BCF 中,
由勾股定理得 BF = √(CF² + BC²) = √(3² + 5²) = √(9 + 25) = √34,
∴ GH = 1/2 BF = √34/2.

20. 如图,在平行四边形$ABCD$中,$AE平分\angle BAC$,$CF平分\angle ACD$。

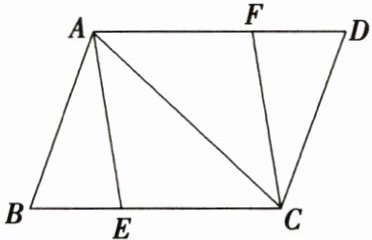
(1) 求证：$\triangle ABE \cong \triangle CDF$；
证明: ∵ 四边形 ABCD 是平行四边形,
∴ AB = CD, ∠B = ∠D, AB // CD,
∴ ∠BAC = ∠ACD,
∵ AE 平分 ∠BAC, CF 平分 ∠ACD,
∴ ∠BAE = ∠CAE = 1/2 ∠BAC,
∠DCF = ∠ACF = 1/2 ∠ACD,
∴ ∠BAE = ∠DCF,
在 △ABE 和 △CDF 中,
{ ∠B = ∠D,
AB = CD,
∠BAE = ∠DCF
}
∴ △ABE ≌ △CDF(ASA);
(2) 当$\triangle ABC$满足AB = AC条件时,四边形$AECF$是矩形？请写出证明过程。
证明: 由 (1) 可知, ∠CAE = ∠ACF, ∴ AE // CF,
∵ △ABE ≌ △CDF, ∴ AE = CF,
∴ 四边形 AECF 是平行四边形,
又 ∵ AB = AC, AE 平分 ∠BAC,
∴ AE ⊥ BC,
∴ ∠AEC = 90°,
∴ 平行四边形 AECF 是矩形.

答案： 20. 解:
(1) 证明:
∵ 四边形 ABCD 是平行四边形,
∴ AB = CD, ∠B = ∠D, AB // CD,
∴ ∠BAC = ∠ACD,
∵ AE 平分 ∠BAC, CF 平分 ∠ACD,
∴ ∠BAE = ∠CAE = 1/2 ∠BAC,
∠DCF = ∠ACF = 1/2 ∠ACD,
∴ ∠BAE = ∠DCF,
在 △ABE 和 △CDF 中,
{ ∠B = ∠D,
AB = CD,
∠BAE = ∠DCF
}
∴ △ABE ≌ △CDF(ASA);
(2) 当 △ABC 满足 AB = AC 时, 四边形 AECF 是矩形, 理由如下:
由
(1) 可知, ∠CAE = ∠ACF,
∴ AE // CF,
∵ △ABE ≌ △CDF,
∴ AE = CF,
∴ 四边形 AECF 是平行四边形,
又
∵ AB = AC, AE 平分 ∠BAC,
∴ AE ⊥ BC,
∴ ∠AEC = 90°,
∴ 平行四边形 AECF 是矩形.