2025年文轩图书假期生活指导暑八年级数学通用版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年文轩图书假期生活指导暑八年级数学通用版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
14. 如图,在$□ ABCD$中,$BD = CD$,$AE \perp BD于点E$,若$\angle C = 70^{\circ}$,则$\angle BAE = $

50
$^{\circ}$。
答案:
14. 50
15. 如图,以$\triangle ABC的三边为边在BC上方分别作等边\triangle ACD$,$\triangle ABE$,$\triangle BCF$。且点$A在\triangle BCF$内部。给出以下结论:① 四边形$ADFE$是平行四边形;② 当$\angle BAC = 150^{\circ}$时,四边形$ADFE$是矩形;③ 当$AB = AC$时,四边形$ADFE$是菱形;④ 当$AB = AC$,且$\angle BAC = 150^{\circ}$时,四边形$ADFE$是正方形。其中正确结论有______

①②③④
(填上所有正确结论的序号)。
答案:
15. ①②③④
16. 如图,四边形$ABCD$是菱形,点$E$,$F分别在AB$,$AD$上,$AE = AF$。求证:$CE = CF$。

证明: 如图, 连接 AC,
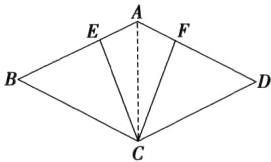
∵ 四边形 ABCD 是菱形,
∴ ∠EAC = ∠FAC,
在 △ACE 和 △ACF 中,
{ AE = AF,
∠EAC = ∠FAC,
AC = AC,
}
∴ △ACE ≌ △ACF(SAS)
∴ CE = CF.

证明: 如图, 连接 AC,

∵ 四边形 ABCD 是菱形,
∴ ∠EAC = ∠FAC,
在 △ACE 和 △ACF 中,
{ AE = AF,
∠EAC = ∠FAC,
AC = AC,
}
∴ △ACE ≌ △ACF(SAS)
∴ CE = CF.
答案:
16. 证明: 如图, 连接 AC,

∵ 四边形 ABCD 是菱形,
∴ ∠EAC = ∠FAC,
在 △ACE 和 △ACF 中,
{ AE = AF,
∠EAC = ∠FAC,
AC = AC,
}
∴ △ACE ≌ △ACF(SAS)
∴ CE = CF.
16. 证明: 如图, 连接 AC,

∵ 四边形 ABCD 是菱形,
∴ ∠EAC = ∠FAC,
在 △ACE 和 △ACF 中,
{ AE = AF,
∠EAC = ∠FAC,
AC = AC,
}
∴ △ACE ≌ △ACF(SAS)
∴ CE = CF.
17. 如图,在四边形$ABCD$中,$AC与BD交于点O$,$BE \perp AC$,$DF \perp AC$,垂足分别为点$E$,$F$,且$BE = DF$,$\angle ABD = \angle BDC$。求证:四边形$ABCD$是平行四边形。
证明: ∵ ∠ABD = ∠BDC,
∴
∴
∵ BE ⊥ AC, DF ⊥ AC
在 △ABE 与 △CDF 中,
{ ∠BAE = ∠DCF,
∠AEB = ∠CFD = 90°,
BE = DF.
}
∴
∴
∴ 四边形 ABCD 是平行四边形.
证明: ∵ ∠ABD = ∠BDC,
∴
AB // CD
.∴
∠BAE = ∠DCF
.∵ BE ⊥ AC, DF ⊥ AC
在 △ABE 与 △CDF 中,
{ ∠BAE = ∠DCF,
∠AEB = ∠CFD = 90°,
BE = DF.
}
∴
△ABE ≌ △CDF(AAS)
.∴
AB = CD
.∴ 四边形 ABCD 是平行四边形.
答案:
17. 证明:
∵ ∠ABD = ∠BDC,
∴ AB // CD.
∴ ∠BAE = ∠DCF.
∵ BE ⊥ AC, DF ⊥ AC
在 △ABE 与 △CDF 中,
{ ∠BAE = ∠DCF,
∠AEB = ∠CFD = 90°,
BE = DF.
}
∴ △ABE ≌ △CDF(AAS).
∴ AB = CD.
∴ 四边形 ABCD 是平行四边形.
∵ ∠ABD = ∠BDC,
∴ AB // CD.
∴ ∠BAE = ∠DCF.
∵ BE ⊥ AC, DF ⊥ AC
在 △ABE 与 △CDF 中,
{ ∠BAE = ∠DCF,
∠AEB = ∠CFD = 90°,
BE = DF.
}
∴ △ABE ≌ △CDF(AAS).
∴ AB = CD.
∴ 四边形 ABCD 是平行四边形.
18. 如图,在矩形$ABCD$中,$AC$是对角线。

(1) 实践与操作:利用尺规作线段$AC$的垂直平分线,垂足为点$O$,交边$AD于点E$,交边$BC于点F$(要求:尺规作图并保留作图痕迹,不写作法,标明字母)。

(2) 猜想与证明:试猜想线段$AE与CF$的数量关系,并加以证明。
AE = CF, 证明如下:
∵ 四边形 ABCD 是矩形, ∴ AD // BC,
∴ ∠EAO = ∠FCO, ∠AEO = ∠CFO,
∵ EF 是 AC 的垂直平分线, ∴ AO = CO,
在 △AOE 和 △COF 中,
{ ∠AEO = ∠CFO,
∠EAO = ∠FCO,
AO = CO
}
∴ △AOE ≌ △COF(AAS),
∴ AE = CF.

(1) 实践与操作:利用尺规作线段$AC$的垂直平分线,垂足为点$O$,交边$AD于点E$,交边$BC于点F$(要求:尺规作图并保留作图痕迹,不写作法,标明字母)。

(2) 猜想与证明:试猜想线段$AE与CF$的数量关系,并加以证明。
AE = CF, 证明如下:
∵ 四边形 ABCD 是矩形, ∴ AD // BC,
∴ ∠EAO = ∠FCO, ∠AEO = ∠CFO,
∵ EF 是 AC 的垂直平分线, ∴ AO = CO,
在 △AOE 和 △COF 中,
{ ∠AEO = ∠CFO,
∠EAO = ∠FCO,
AO = CO
}
∴ △AOE ≌ △COF(AAS),
∴ AE = CF.
答案:
18. 解:
(1) 如图,

(2) AE = CF, 证明如下:
∵ 四边形 ABCD 是矩形,
∴ AD // BC,
∴ ∠EAO = ∠FCO, ∠AEO = ∠CFO,
∵ EF 是 AC 的垂直平分线,
∴ AO = CO,
在 △AOE 和 △COF 中,
{ ∠AEO = ∠CFO,
∠EAO = ∠FCO,
AO = CO
}
∴ △AOE ≌ △COF(AAS),
∴ AE = CF.
18. 解:
(1) 如图,

(2) AE = CF, 证明如下:
∵ 四边形 ABCD 是矩形,
∴ AD // BC,
∴ ∠EAO = ∠FCO, ∠AEO = ∠CFO,
∵ EF 是 AC 的垂直平分线,
∴ AO = CO,
在 △AOE 和 △COF 中,
{ ∠AEO = ∠CFO,
∠EAO = ∠FCO,
AO = CO
}
∴ △AOE ≌ △COF(AAS),
∴ AE = CF.
查看更多完整答案,请扫码查看


