2025年文轩图书假期生活指导暑八年级数学通用版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年文轩图书假期生活指导暑八年级数学通用版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
16. 在平面直角坐标系内有三点$A(-1,4)$,$B(-3,2)$,$C(0,6)$.
(1)求过其中两点的直线的函数表达式(选一种情形作答);
(2)判断A,B,C三点是否在同一直线上,并说明理由.
(1)求过其中两点的直线的函数表达式(选一种情形作答);
(2)判断A,B,C三点是否在同一直线上,并说明理由.
答案:
解:
(1)设A(−1,4),B(−3,2)两点所在直线解析式为y = kx + b。
∴$\begin{cases}-k + b = 4\\-3k + b = 2\end{cases}$,解得$\begin{cases}k = 1\\b = 5\end{cases}$。
∴直线AB的解析式为y = x + 5。
(2)当x = 0时,y = 0 + 5 ≠ 6。
∴点C(0,6)不在直线AB上,即点A,B,C三点不在同一条直线上。
(1)设A(−1,4),B(−3,2)两点所在直线解析式为y = kx + b。
∴$\begin{cases}-k + b = 4\\-3k + b = 2\end{cases}$,解得$\begin{cases}k = 1\\b = 5\end{cases}$。
∴直线AB的解析式为y = x + 5。
(2)当x = 0时,y = 0 + 5 ≠ 6。
∴点C(0,6)不在直线AB上,即点A,B,C三点不在同一条直线上。
17. 李强用甲、乙两种具有恒温功能的热水壶同时加热相同质量的水,甲壶比乙壶加热速度快.在一段时间内,水温$y(^{\circ }C)与加热时间x(s)$之间近似满足一次函数关系,根据记录的数据,画函数图象如下:
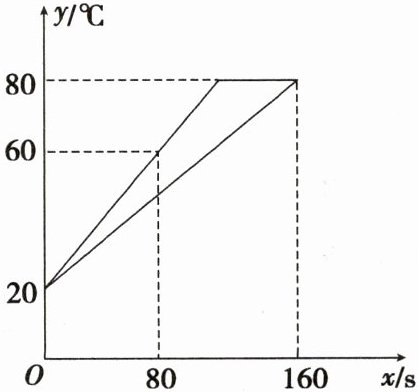
(1)加热前水温是____
(2)求乙壶中水温y关于加热时间x的函数解析式;
(3)当甲壶中水温刚达到$80^{\circ }C$时,乙壶中水温是____

(1)加热前水温是____
20
$^{\circ }C$;(2)求乙壶中水温y关于加热时间x的函数解析式;
(3)当甲壶中水温刚达到$80^{\circ }C$时,乙壶中水温是____
65
$^{\circ }C$.
答案:
解:
(1)由图象得x = 0时y = 20。
∴加热前水温是$20^{\circ}C$。
故答案为:20。
(2)设乙壶中水温y关于加热时间x的函数解析式为y = kx + b。
将(0,20),(160,80)代入y = kx + b得$\begin{cases}20 = b\\80 = 160k + b\end{cases}$,解得$\begin{cases}k = \frac{3}{8}\\b = 20\end{cases}$。
∴$y = \frac{3}{8}x + 20$。
(3)甲水壶的加热速度为$(60 - 20)÷80 = \frac{1}{2}^{\circ}C/s$。
∴甲水壶中温度为$80^{\circ}C$时,加热时间为$(80 - 20)÷\frac{1}{2} = 120s$。
将x = 120代入$y = \frac{3}{8}x + 20$得y = 65。
故答案为:65。
(1)由图象得x = 0时y = 20。
∴加热前水温是$20^{\circ}C$。
故答案为:20。
(2)设乙壶中水温y关于加热时间x的函数解析式为y = kx + b。
将(0,20),(160,80)代入y = kx + b得$\begin{cases}20 = b\\80 = 160k + b\end{cases}$,解得$\begin{cases}k = \frac{3}{8}\\b = 20\end{cases}$。
∴$y = \frac{3}{8}x + 20$。
(3)甲水壶的加热速度为$(60 - 20)÷80 = \frac{1}{2}^{\circ}C/s$。
∴甲水壶中温度为$80^{\circ}C$时,加热时间为$(80 - 20)÷\frac{1}{2} = 120s$。
将x = 120代入$y = \frac{3}{8}x + 20$得y = 65。
故答案为:65。
18. 根据市场需求,某书城准备购进甲、乙两种青少年喜欢的读本进行销售,进价和售价分别如下.
|读本|进价/(元/本)|售价/(元/本)|
|甲|30|45|
|乙|20|30|
现计划用不超过1850元购进这两种读本共80本,并将这80本读本全部售完.设购进甲种读本x本,这两种读本的总利润为y元.
(1)写出y与x之间的函数关系式;
(2)该书城如何进货才能获得最大利润?最大利润是多少?
|读本|进价/(元/本)|售价/(元/本)|
|甲|30|45|
|乙|20|30|
现计划用不超过1850元购进这两种读本共80本,并将这80本读本全部售完.设购进甲种读本x本,这两种读本的总利润为y元.
(1)写出y与x之间的函数关系式;
(2)该书城如何进货才能获得最大利润?最大利润是多少?
答案:
解:
(1)$y = (45 - 30)x + (30 - 20)(80 - x) = 5x + 800$。
(2)
∵计划用不超过1850元购进这两种读本共80本。
∴$30x + 20(80 - x) \leq 1850$。
解得$x \leq 25$。
∵$5 > 0$,
∴y随x的增大而增大。
∴当x = 25时,y有最大值。
$y_{最大} = 5×25 + 800 = 925$(元)。
$80 - 25 = 55$(本)。
答:购进甲种读本25本,乙种读本55本才能获得最大利润,最大利润为925元。
(1)$y = (45 - 30)x + (30 - 20)(80 - x) = 5x + 800$。
(2)
∵计划用不超过1850元购进这两种读本共80本。
∴$30x + 20(80 - x) \leq 1850$。
解得$x \leq 25$。
∵$5 > 0$,
∴y随x的增大而增大。
∴当x = 25时,y有最大值。
$y_{最大} = 5×25 + 800 = 925$(元)。
$80 - 25 = 55$(本)。
答:购进甲种读本25本,乙种读本55本才能获得最大利润,最大利润为925元。
查看更多完整答案,请扫码查看


