《2025年启东中学作业本八年级数学上册苏科版连淮专版》

2. 如图,$AD= BE,BD= CE$,B 是 AC 的中点,求证:$\triangle ABD\cong \triangle BCE.$

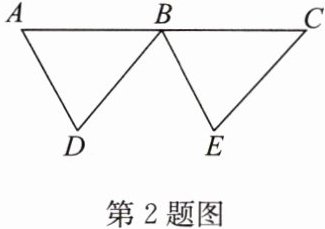
答案： 解：因为$B$是$AC$的中点，所以$AB = BC$。
在$\triangle ABD$和$\triangle BCE$中，
$\begin{cases}AD = BE \\BD = CE \\AB = BC\end{cases}$
根据“边边边”（$SSS$）全等判定定理，可得$\triangle ABD\cong\triangle BCE$。

3. 如图,点 A,C,F,B 在同一条直线上,$AC= BF,AE= BD,EF= CD.$
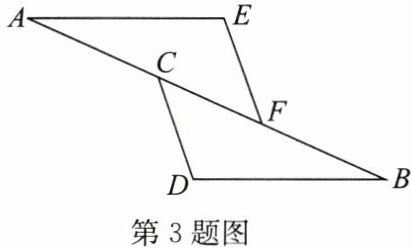
求证:$∠AFE= ∠BCD.$

答案： 解：
因为$AC = BF$，所以$AC + CF = BF + CF$，即$AF = BC$。
在$\triangle AFE$和$\triangle BCD$中，
$\begin{cases}AF = BC \\AE = BD \\EF = CD\end{cases}$
根据“边边边”（$SSS$）全等判定定理，可得$\triangle AFE\cong\triangle BCD$。
因为全等三角形的对应角相等，所以$\angle AFE = \angle BCD$。
综上，$\angle AFE = \angle BCD$得证。

1. 判定两个三角形全等的方法有SAS,ASA,AAS,SSS。

答案： SAS ASA AAS SSS

2. 判定两个三角形全等,至少有一个条件是边。

答案： 边

1. 如图,点 A,B,C,D 在一条直线上,且 $ AB = CD $,$ AE = BF $,$ CE = DF $。求证：$ ∠E = ∠F $。

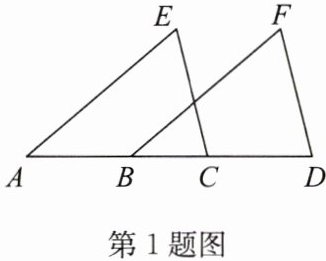
答案： 解：
因为$AB = CD$，所以$AB + BC = CD + BC$，即$AC = BD$。
在$\triangle ACE$和$\triangle BDF$中，
$\begin{cases}AC = BD\\AE = BF\\CE = DF\end{cases}$
根据$SSS$（边边边）全等判定定理，可得$\triangle ACE\cong\triangle BDF$。
因为全等三角形的对应角相等，所以$\angle E=\angle F$。

2. 如图,点 A,B,C,D 在一条直线上,$ AE // DF $,$ EC // BF $,$ AB = CD $。求证：$ AE = DF $。

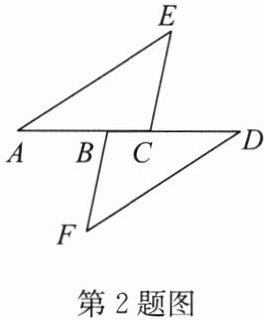
答案： 解：
因为$AE// DF$，所以$\angle A=\angle D$（两直线平行，内错角相等）。
因为$EC// BF$，所以$\angle ECA=\angle FBD$（两直线平行，内错角相等）。
又因为$AB = CD$，所以$AB + BC=CD + BC$，即$AC = DB$。
在$\triangle AEC$和$\triangle DFB$中，
$\begin{cases}\angle A=\angle D\\AC = DB\\\angle ECA=\angle FBD\end{cases}$
所以$\triangle AEC\cong\triangle DFB$（$ASA$）。
所以$AE = DF$（全等三角形对应边相等）。