《2025年启东中学作业本八年级数学上册苏科版连淮专版》

1. 线段是轴对称图形,线段的垂直平分线是它的对称轴。

答案： 线段的垂直平分线

2. 线段垂直平分线的性质定理：线段垂直平分线上的点到线段两端的距离相等。

答案： 相等

3. 线段垂直平分线性质定理的逆定理：到线段两端距离相等的点在线段的垂直平分线上。

答案： 到线段两端距离相等

4. 三角形三条边的垂直平分线相交于同一点,这个点到三角形三个顶点的距离相等。

答案： 三个顶点

1. 如图,在$\triangle ABC$中,线段$AB的垂直平分线交AB于点D$,交$AC于点E$,连接$BE$。
(1)若$\triangle ADE的周长是11$,$DE = 2$,求$\triangle ABE$的周长；
(2)若$\angle A = 23^{\circ}$,$BE = BC$,求$\angle C$的度数。

答案： 解:
(1)
∵DE垂直平分AB,
∴AE=BE,AD=BD.
∵△ADE的周长为AE+AD+DE=11,DE=2,
∴AE+AD=BE+BD=9,
∴△ABE的周长为AE+BE+AD+BD=18.
(2)
∵AE=BE,∠A=23°,
∴∠ABE=∠A=23°,
∴∠AEB=180°-∠A-∠ABE=134°,
∴∠BEC=46°.
∵BE=BC,
∴∠C=∠BEC=46°.

2. 如图,在$\triangle ABC$中,$AB的垂直平分线分别交AB$,$BC于点D$,$E$,$AC的垂直平分线分别交AC$,$BC于点F$,$G$。
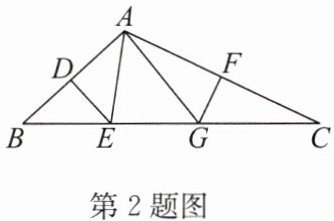
(1)若$BC = 9$,求$\triangle AEG$的周长；
(2)若$\angle BAC = 130^{\circ}$,求$\angle EAG$的度数。

答案： 解:
(1)
∵DE是AB的垂直平分线,GF是AC的垂直平分线,
∴EA=EB,GA=GC,
∴△AEG的周长为EA+EG+GA=EB+EG+GC=BC=9.
(2)
∵∠BAC=130°,
∴∠B+∠C=180°-130°=50°.
∵EA=EB,GA=GC,
∴∠EAB=∠B,∠GAC=∠C,
∴∠EAB+∠GAC=∠B+∠C=50°,
∴∠EAG=130°-50°=80°.

3. 如图,$BA平分\angle CBD$,$AB平分\angle CAD$。求证：$AB垂直平分CD$。

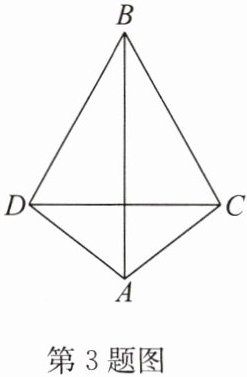
答案： 解：
因为$BA$平分$\angle CBD$，所以$\angle ABD = \angle ABC$。
因为$AB$平分$\angle CAD$，所以$\angle BAD = \angle BAC$。
在$\triangle ABD$和$\triangle ABC$中：
$\begin{cases}\angle ABD = \angle ABC \\ AB = AB \\ \angle BAD = \angle BAC\end{cases}$
根据$ASA$（角边角）定理可得$\triangle ABD\cong\triangle ABC$。
所以$AD = AC$，$BD = BC$。
这表明点$A$在线段$CD$的垂直平分线上（到一条线段两个端点距离相等的点，在这条线段的垂直平分线上），点$B$也在线段$CD$的垂直平分线上。
由于两点确定一条直线，所以$AB$是线段$CD$的垂直平分线，即$AB$垂直平分$CD$。