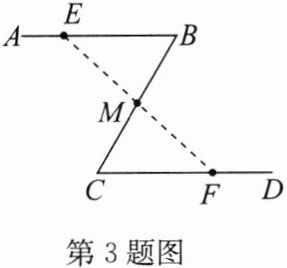
3.如图,公园有一条“Z"字形道路AB一BC一CD,其中AB//CD,在E,M,F处各有一个
小石凳,且BE= CF,M为BC的中点,连接EM,MF,请问石凳M到石凳E,F的距离
ME,MF是否相等?并说明理由.
小石凳,且BE= CF,M为BC的中点,连接EM,MF,请问石凳M到石凳E,F的距离
ME,MF是否相等?并说明理由.

答案:
解:$ME = MF$,理由如下:
因为$AB// CD$,所以$\angle B=\angle C$(两直线平行,内错角相等)。
又因为$M$为$BC$的中点,所以$BM = CM$。
在$\triangle BEM$和$\triangle CFM$中,$\begin{cases}BE = CF\\\angle B=\angle C\\BM = CM\end{cases}$,
所以$\triangle BEM\cong\triangle CFM$($SAS$)。
所以$ME = MF$(全等三角形的对应边相等)。
综上,石凳$M$到石凳$E$,$F$的距离$ME$,$MF$相等。
因为$AB// CD$,所以$\angle B=\angle C$(两直线平行,内错角相等)。
又因为$M$为$BC$的中点,所以$BM = CM$。
在$\triangle BEM$和$\triangle CFM$中,$\begin{cases}BE = CF\\\angle B=\angle C\\BM = CM\end{cases}$,
所以$\triangle BEM\cong\triangle CFM$($SAS$)。
所以$ME = MF$(全等三角形的对应边相等)。
综上,石凳$M$到石凳$E$,$F$的距离$ME$,$MF$相等。
1. 基本事实:
两角及其夹边
分别相等的两个三角形全等(简写成“角边角”或“ASA
”).
答案:
两角及其夹边 ASA
2. 符号语言:
∵∠A=
∴△ABC≌△DEF(
∵∠A=
∠D
,AB=DE
,∠B=∠E
,∴△ABC≌△DEF(
ASA
)
答案:
∠D DE ∠B=∠E ASA
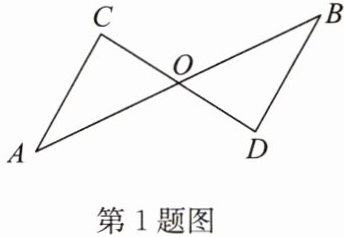
1. 如图,$AB$,$CD相交于点O$,且$O是AB$的中点,$∠A= ∠B$. 求证:$\triangle AOC≌\triangle BOD$.

答案:
解:
因为$O$是$AB$的中点,所以$OA = OB$。
在$\triangle AOC$和$\triangle BOD$中,
$\begin{cases}∠A = ∠B\\OA = OB\\∠AOC = ∠BOD(对顶角相等)\end{cases}$
根据$ASA$(角 - 边 - 角)判定定理,可得$\triangle AOC≌\triangle BOD$。
因为$O$是$AB$的中点,所以$OA = OB$。
在$\triangle AOC$和$\triangle BOD$中,
$\begin{cases}∠A = ∠B\\OA = OB\\∠AOC = ∠BOD(对顶角相等)\end{cases}$
根据$ASA$(角 - 边 - 角)判定定理,可得$\triangle AOC≌\triangle BOD$。
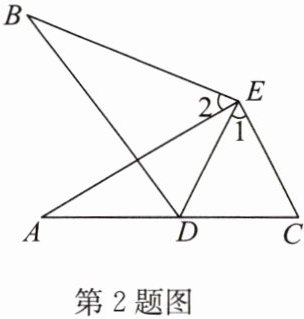
2. 如图,$∠A= ∠B$,$AE= BE$,$∠1= ∠2$,点$D在AC$边上.
求证:$\triangle AEC≌\triangle BED$.
求证:$\triangle AEC≌\triangle BED$.

答案:
解:因为$\angle1 = \angle2$,
所以$\angle1 + \angle AED = \angle2 + \angle AED$,
即$\angle AEC = \angle BED$。
在$\triangle AEC$和$\triangle BED$中,
$\begin{cases}\angle A = \angle B \\AE = BE \\\angle AEC = \angle BED\end{cases}$
根据$ASA$(两角及其夹边对应相等的两个三角形全等),
可得$\triangle AEC≌\triangle BED$。
所以$\angle1 + \angle AED = \angle2 + \angle AED$,
即$\angle AEC = \angle BED$。
在$\triangle AEC$和$\triangle BED$中,
$\begin{cases}\angle A = \angle B \\AE = BE \\\angle AEC = \angle BED\end{cases}$
根据$ASA$(两角及其夹边对应相等的两个三角形全等),
可得$\triangle AEC≌\triangle BED$。
查看更多完整答案,请扫码查看


