《2025年启东中学作业本八年级数学上册苏科版连淮专版》

1. 三边都相等的三角形叫作等边三角形.

答案： 三边都相等

2. 等边三角形的性质定理:等边三角形的各角都等于60°.

答案： 60°

3. 等边三角形的判定定理:
(1)三个角都相等的三角形是等边三角形.
(2)有一个角是$60^{\circ}$的等腰三角形是等边三角形.

答案：
(1)相等
(2)等腰

4. 在直角三角形中,如果一个锐角等于$30^{\circ}$,那么它所对的直角边是斜边的一半.

答案： 一半

1. 下列条件中,不能得到等边三角形的是 (D)
A.有两个内角是$60^{\circ}$的三角形
B.三边都相等的三角形
C.有一个角是$60^{\circ}$的等腰三角形
D.有两个外角相等的等腰三角形

答案： D

2. 在$Rt\triangle ABC$中,$∠C = 90^{\circ}$,$∠B = 30^{\circ}$,$AB = 8cm$,则$AC$的长度为 (A)
A.4 cm
B.5 cm
C.6 cm
D.16 cm

答案： A

3. 如图,在等边$\triangle ABC$中,$DE// BA分别交BC$,$AC于点D$,$E$. 求证:$\triangle CDE$是等边三角形.

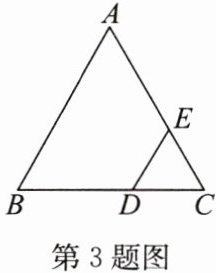
答案： 证明:
∵△ABC是等边三角形，
∴∠A=∠B=∠C=60°.
∵DE//BA,
∴∠CED=∠A=60°,∠CDE=∠B=60°,
∴∠CDE=∠CED=∠C,
∴△CDE是等边三角形.

4. 如图,在等边$\triangle ABC$中,$M是BC$的中点,$MN\perp AB$,垂足为$N$,连接$AM$,求证:$AM = 2MN$.

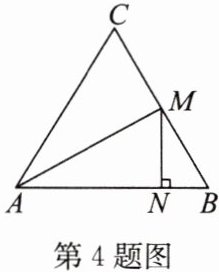
答案： 证明:
∵△ABC是等边三角形，
∴∠BAC=60°,AB=AC.
∵M是BC的中点,
∴∠BAM=$\frac{1}{2}$∠BAC=30°.
又
∵MN⊥AB,
∴AM=2MN.

5. 如图,在$\triangle ABC$中,$AB = AC$,$D为AB$边的中点,$DE\perp AC于点E$,$DF\perp BC于点F$,$DE = DF$. 求证:$\triangle ABC$是等边三角形.

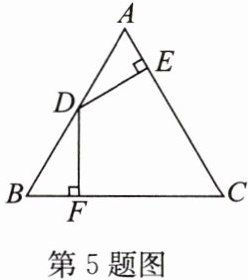
答案： 证明:
∵D为AB的中点,
∴AD=BD.
∵DE⊥AC,DF⊥BC,
∴∠AED=∠BFD=90°.
在Rt△ADE和Rt△BDF中,$\left\{\begin{array}{l} AD=BD,\\ DE=DF,\end{array}\right.$
∴Rt△ADE≌Rt△BDF(HL),
∴∠A=∠B,
∴CA=CB.
∵AB=AC,
∴AB=BC=AC,
∴△ABC是等边三角形.