《2025年启东中学作业本八年级数学上册苏科版连淮专版》

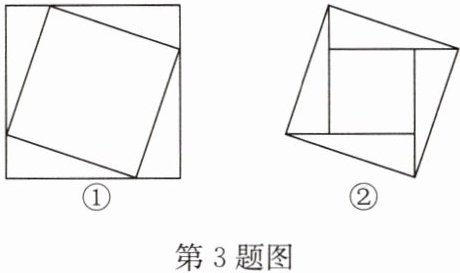
3. 如图,两图均由四个全等的直角三角形拼接而成,且直角三角形的两条直角边长分别为a,b,斜边长为c,$b＞a$. 请选择一个你喜欢的图形,利用等面积法验证勾股定理.

答案： 解:(答案不唯一)选择题图②,验证如下:
∵S大正方形=c²,S大正方形=4S三角形+S小正方形=4×$\frac{1}{2}$ab+(b-a)²,
∴c²=4×$\frac{1}{2}$ab+(b-a)²,
整理,得c²=2ab+b²-2ab+a²,即c²=a²+b².

4. 先阅读材料,再解决问题:
三国时期吴国的数学家赵爽创建了一幅“弦图”,利用面积法给出了勾股定理的证明,实际上,该“弦图”与完全平方公式有着密切的关系. 如图,这是由8个全等的直角边长分别为a,b,斜边长为c的三角形拼成的“弦图”.
(1)正方形ABCD的面积可表示为(a+b)²,正方形PQMN的面积可表示为(a-b)²;(用含a,b的式子表示)
(2)请结合图形用面积法说明$(a+b)^{2},ab,(a-b)^{2}$三者之间的等量关系;
解:∵S正方形ABCD=S正方形MNPQ+8S△DEH,
∴(a+b)²=(a-b)²+$\frac{1}{2}$ab×8,
∴(a+b)²=(a-b)²+4ab.
(3)若$a+b= 7,ab= 5$,求正方形EFGH的面积.
解:∵S正方形EFGH=S正方形ABCD-4S△DEH,
∴S正方形EFGH=(a+b)²-$\frac{1}{2}$ab×4=(a+b)²-2ab=7²-2×5=39.

答案：
(1)(a+b)² (a-b)²
(2)解:
∵S正方形ABCD=S正方形MNPQ+8S△DEH,
∴(a+b)²=(a-b)²+$\frac{1}{2}$ab×8,
∴(a+b)²=(a-b)²+4ab.
(3)解:
∵S正方形EFGH=S正方形ABCD-4S△DEH,
∴S正方形EFGH=(a+b)²-$\frac{1}{2}$ab×4=(a+b)²-2ab=7²-2×5=39.

1. 勾股定理的逆定理：如果三角形的三边长分别为 $ a,b,c $,且$a^{2}+b^{2}=c^{2}$,那么这个三角形是直角三角形。

答案： $a^{2}+b^{2}=c^{2}$

2. 如果三个正整数 $ a,b,c $ 满足关系$a^{2}+b^{2}=c^{2}$,则称 $ a,b,c $ 为勾股数。

答案： $a^{2}+b^{2}=c^{2}$

1. 下列各组数据为三角形的三边长,其中能构成直角三角形的是 (C)
A.$ 4 \mathrm { cm }, 8 \mathrm { cm }, 7 \mathrm { cm } $
B.$ 3 \mathrm { cm }, 3 \mathrm { cm }, 3 \mathrm { cm } $
C.$ 6 \mathrm { cm }, 10 \mathrm { cm }, 8 \mathrm { cm } $
D.$ 2 \mathrm { cm }, 2 \mathrm { cm }, 3 \mathrm { cm } $

答案： C

2. 下列各组数不是勾股数的是 (D)
A.$ 3,4,5 $
B.$ 5,12,13 $
C.$ 7,24,25 $
D.$ 0.6,0.8,1 $

答案： D