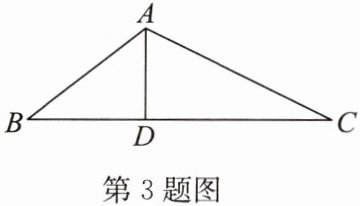
3. 如图,$ D $ 为 $ \triangle A B C $ 的边 $ B C $ 上的一点,$ A B = 10 $,$ A D = 6 $,$ D C = 2 A D $,$ B D = \frac { 2 } { 3 } D C $。
求:(1)$ B C $ 的长;
(2)$ \triangle A B C $ 的面积。
求:(1)$ B C $ 的长;
(2)$ \triangle A B C $ 的面积。

答案:
解:
(1)
∵AD=6,DC=2AD,
∴DC=12.
∵BD=$\frac{2}{3}$DC,
∴BD=8,BC=BD+DC=8+12=20.
(2)在△ABD中,AB=10,AD=6,BD=8,
∴AB²=AD²+BD²,
∴△ABD为直角三角形,且∠ADB=90°,即AD⊥BC;
∵BC=20,AD=6,
∴S△ABC=$\frac{1}{2}$×20×6=60.
(1)
∵AD=6,DC=2AD,
∴DC=12.
∵BD=$\frac{2}{3}$DC,
∴BD=8,BC=BD+DC=8+12=20.
(2)在△ABD中,AB=10,AD=6,BD=8,
∴AB²=AD²+BD²,
∴△ABD为直角三角形,且∠ADB=90°,即AD⊥BC;
∵BC=20,AD=6,
∴S△ABC=$\frac{1}{2}$×20×6=60.
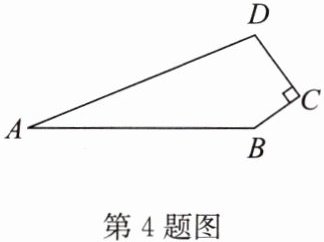
4. 如图,$ \angle C = 90 ^ { \circ } $,$ A B = 12 $,$ B C = 3 $,$ C D = 4 $,$ A D = 13 $,求四边形 $ A B C D $ 的面积。

答案:
1. 首先,连接$BD$:
在$Rt\triangle BCD$中,根据勾股定理$a^{2}+b^{2}=c^{2}$(其中$a = BC$,$b = CD$,$c = BD$):
已知$\angle C = 90^{\circ}$,$BC = 3$,$CD = 4$,则$BD=\sqrt{BC^{2}+CD^{2}}$。
代入数值可得$BD=\sqrt{3^{2}+4^{2}}=\sqrt{9 + 16}=\sqrt{25}=5$。
在$\triangle ABD$中:
已知$AB = 12$,$BD = 5$,$AD = 13$。
计算$AB^{2}+BD^{2}$和$AD^{2}$的值:
$AB^{2}+BD^{2}=12^{2}+5^{2}=144 + 25=169$,$AD^{2}=13^{2}=169$。
所以$AB^{2}+BD^{2}=AD^{2}$。
根据勾股定理的逆定理(若$a^{2}+b^{2}=c^{2}$,则以$a$,$b$,$c$为边的三角形是直角三角形,其中$c$为斜边),可知$\angle ABD = 90^{\circ}$。
2. 然后,计算四边形$ABCD$的面积:
四边形$ABCD$的面积$S = S_{\triangle ABD}+S_{\triangle BCD}$。
根据三角形面积公式$S=\frac{1}{2}ah$(对于直角三角形,$S=\frac{1}{2}×$一条直角边$×$另一条直角边):
对于$\triangle ABD$,$S_{\triangle ABD}=\frac{1}{2}AB\cdot BD$,其中$AB = 12$,$BD = 5$,则$S_{\triangle ABD}=\frac{1}{2}×12×5 = 30$。
对于$\triangle BCD$,$S_{\triangle BCD}=\frac{1}{2}BC\cdot CD$,其中$BC = 3$,$CD = 4$,则$S_{\triangle BCD}=\frac{1}{2}×3×4 = 6$。
所以$S = S_{\triangle ABD}+S_{\triangle BCD}=30 + 6=36$。
故四边形$ABCD$的面积为$36$。
在$Rt\triangle BCD$中,根据勾股定理$a^{2}+b^{2}=c^{2}$(其中$a = BC$,$b = CD$,$c = BD$):
已知$\angle C = 90^{\circ}$,$BC = 3$,$CD = 4$,则$BD=\sqrt{BC^{2}+CD^{2}}$。
代入数值可得$BD=\sqrt{3^{2}+4^{2}}=\sqrt{9 + 16}=\sqrt{25}=5$。
在$\triangle ABD$中:
已知$AB = 12$,$BD = 5$,$AD = 13$。
计算$AB^{2}+BD^{2}$和$AD^{2}$的值:
$AB^{2}+BD^{2}=12^{2}+5^{2}=144 + 25=169$,$AD^{2}=13^{2}=169$。
所以$AB^{2}+BD^{2}=AD^{2}$。
根据勾股定理的逆定理(若$a^{2}+b^{2}=c^{2}$,则以$a$,$b$,$c$为边的三角形是直角三角形,其中$c$为斜边),可知$\angle ABD = 90^{\circ}$。
2. 然后,计算四边形$ABCD$的面积:
四边形$ABCD$的面积$S = S_{\triangle ABD}+S_{\triangle BCD}$。
根据三角形面积公式$S=\frac{1}{2}ah$(对于直角三角形,$S=\frac{1}{2}×$一条直角边$×$另一条直角边):
对于$\triangle ABD$,$S_{\triangle ABD}=\frac{1}{2}AB\cdot BD$,其中$AB = 12$,$BD = 5$,则$S_{\triangle ABD}=\frac{1}{2}×12×5 = 30$。
对于$\triangle BCD$,$S_{\triangle BCD}=\frac{1}{2}BC\cdot CD$,其中$BC = 3$,$CD = 4$,则$S_{\triangle BCD}=\frac{1}{2}×3×4 = 6$。
所以$S = S_{\triangle ABD}+S_{\triangle BCD}=30 + 6=36$。
故四边形$ABCD$的面积为$36$。
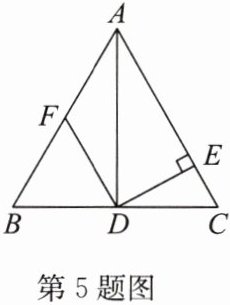
5. 如图,$ A D $ 是 $ \triangle A B C $ 的中线,$ D E \perp A C $ 于点 $ E $,$ D F $ 是 $ \triangle A B D $ 的中线,且 $ C E = 2 $,$ D E = 4 $,$ A E = 8 $。
(1)求证:$ \angle A D C = 90 ^ { \circ } $;
(2)求 $ D F $ 的长。
(1)求证:$ \angle A D C = 90 ^ { \circ } $;
(2)求 $ D F $ 的长。

答案:
1. (1)证明$\angle ADC = 90^{\circ}$:
解:在$Rt\triangle ADE$中,根据勾股定理$a^{2}+b^{2}=c^{2}$(其中$a = DE$,$b = AE$,$c = AD$),可得$AD=\sqrt{AE^{2}+DE^{2}}$。
已知$AE = 8$,$DE = 4$,则$AD=\sqrt{8^{2}+4^{2}}=\sqrt{64 + 16}=\sqrt{80}=4\sqrt{5}$。
因为$AD$是$\triangle ABC$的中线,所以$BD = CD$。
在$Rt\triangle CDE$中,根据勾股定理$CD=\sqrt{CE^{2}+DE^{2}}$,已知$CE = 2$,$DE = 4$,则$CD=\sqrt{2^{2}+4^{2}}=\sqrt{4 + 16}=\sqrt{20}=2\sqrt{5}$。
在$\triangle ADC$中,$AD = 4\sqrt{5}$,$CD = 2\sqrt{5}$,$AC=AE + CE=8 + 2 = 10$。
验证勾股定理逆定理:$AD^{2}+CD^{2}=(4\sqrt{5})^{2}+(2\sqrt{5})^{2}=80 + 20 = 100$,$AC^{2}=10^{2}=100$。
所以$AD^{2}+CD^{2}=AC^{2}$,根据勾股定理逆定理$\left(\right.$若$a^{2}+b^{2}=c^{2}$,则以$a$,$b$,$c$为边的三角形是直角三角形,其中$c$为斜边$\left.\right)$,可得$\angle ADC = 90^{\circ}$。
2. (2)求$DF$的长:
解:因为$AD$是$\triangle ABC$的中线,$\angle ADC = 90^{\circ}$,所以$BD = CD = 2\sqrt{5}$,$AB=\sqrt{AD^{2}+BD^{2}}$($\angle ADB = 90^{\circ}$,因为$\angle ADC = 90^{\circ}$,$B$,$D$,$C$共线),$AD = 4\sqrt{5}$,$BD = 2\sqrt{5}$,则$AB=\sqrt{(4\sqrt{5})^{2}+(2\sqrt{5})^{2}}=\sqrt{80 + 20}=\sqrt{100}=10$。
又因为$DF$是$\triangle ABD$的中线,在$Rt\triangle ABD$中,根据直角三角形斜边中线定理$\left(\right.$直角三角形斜边中线等于斜边的一半$\left.\right)$,所以$DF=\frac{1}{2}AB$。
所以$DF = 5$。
综上,(1)已证$\angle ADC = 90^{\circ}$;(2)$DF$的长为$5$。
解:在$Rt\triangle ADE$中,根据勾股定理$a^{2}+b^{2}=c^{2}$(其中$a = DE$,$b = AE$,$c = AD$),可得$AD=\sqrt{AE^{2}+DE^{2}}$。
已知$AE = 8$,$DE = 4$,则$AD=\sqrt{8^{2}+4^{2}}=\sqrt{64 + 16}=\sqrt{80}=4\sqrt{5}$。
因为$AD$是$\triangle ABC$的中线,所以$BD = CD$。
在$Rt\triangle CDE$中,根据勾股定理$CD=\sqrt{CE^{2}+DE^{2}}$,已知$CE = 2$,$DE = 4$,则$CD=\sqrt{2^{2}+4^{2}}=\sqrt{4 + 16}=\sqrt{20}=2\sqrt{5}$。
在$\triangle ADC$中,$AD = 4\sqrt{5}$,$CD = 2\sqrt{5}$,$AC=AE + CE=8 + 2 = 10$。
验证勾股定理逆定理:$AD^{2}+CD^{2}=(4\sqrt{5})^{2}+(2\sqrt{5})^{2}=80 + 20 = 100$,$AC^{2}=10^{2}=100$。
所以$AD^{2}+CD^{2}=AC^{2}$,根据勾股定理逆定理$\left(\right.$若$a^{2}+b^{2}=c^{2}$,则以$a$,$b$,$c$为边的三角形是直角三角形,其中$c$为斜边$\left.\right)$,可得$\angle ADC = 90^{\circ}$。
2. (2)求$DF$的长:
解:因为$AD$是$\triangle ABC$的中线,$\angle ADC = 90^{\circ}$,所以$BD = CD = 2\sqrt{5}$,$AB=\sqrt{AD^{2}+BD^{2}}$($\angle ADB = 90^{\circ}$,因为$\angle ADC = 90^{\circ}$,$B$,$D$,$C$共线),$AD = 4\sqrt{5}$,$BD = 2\sqrt{5}$,则$AB=\sqrt{(4\sqrt{5})^{2}+(2\sqrt{5})^{2}}=\sqrt{80 + 20}=\sqrt{100}=10$。
又因为$DF$是$\triangle ABD$的中线,在$Rt\triangle ABD$中,根据直角三角形斜边中线定理$\left(\right.$直角三角形斜边中线等于斜边的一半$\left.\right)$,所以$DF=\frac{1}{2}AB$。
所以$DF = 5$。
综上,(1)已证$\angle ADC = 90^{\circ}$;(2)$DF$的长为$5$。
用勾股定理及其逆定理解决实际问题的关键是构造出
直角
三角形.
答案:
直角
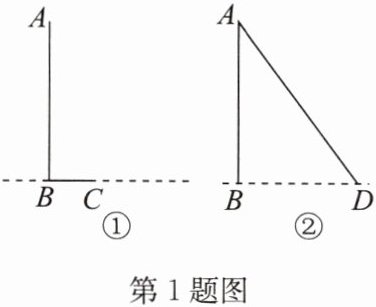
1. 数学兴趣小组要测量旗杆的高度,同学们发现系在旗杆顶端 A 的绳子沿旗杆垂到地面时,测得多出部分 BC 的长为 2 m(如图①),再将绳子拉直(如图②),测得绳子末端的位置 D 到旗杆底部 B 的距离为 6 m,求旗杆 AB 的高.

答案:
解:设旗杆AB的高为x m.
根据题意,得∠ABD=90°,BD=6 m,AD=(x+2)m.
在Rt△ABD中,∠ABD=90°,
∴AB²+BD²=AD²,
∴x²+6²=(x+2)²,
解得x=8.
答:旗杆AB的高为8 m.
根据题意,得∠ABD=90°,BD=6 m,AD=(x+2)m.
在Rt△ABD中,∠ABD=90°,
∴AB²+BD²=AD²,
∴x²+6²=(x+2)²,
解得x=8.
答:旗杆AB的高为8 m.
查看更多完整答案,请扫码查看


