《2025年启东中学作业本八年级数学上册苏科版连淮专版》

1. 角是轴对称图形,角平分线所在的直线是它的对称轴.

答案： 角平分线所在的直线

2. 角平分线的性质定理：角平分线上的点到角两边的距离相等.

答案： 相等

3. 角平分线性质定理的逆定理：角的内部到角两边距离相等的点在角的平分线上.

答案： 角的平分线上

4. 三角形三个角的平分线相交于同一点,这个点到三角形三边的距离相等.

答案： 三边

1. 如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,若$BD平分\angle ABC$,$AC = 12$,$AD = 3CD$,则点$D到AB$的距离为3.

答案： 3

2. 如图,在$\triangle ABC$中,$AD是\angle BAC$的平分线,$E$,$F分别是AB$,$AC$上的点,且$\angle AED + \angle AFD = 180^{\circ}$. 求证：$DE = DF$.

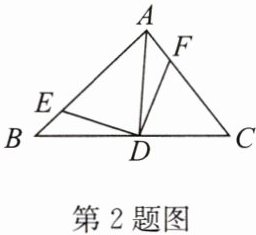
答案： 解：过点$D$作$DM\perp AB$于点$M$，$DN\perp AC$于点$N$。
因为$AD$是$\angle BAC$的平分线，根据角平分线的性质：角平分线上的点到角两边的距离相等，所以$DM = DN$。
因为$\angle AED+\angle AFD = 180^{\circ}$，$\angle AFD+\angle DFN=180^{\circ}$（邻补角定义），所以$\angle AED=\angle DFN$。
在$\triangle DEM$和$\triangle DFN$中，$\left\{\begin{array}{l}\angle DME=\angle DNF = 90^{\circ}\\\angle DEM=\angle DFN\\DM = DN\end{array}\right.$。
根据$AAS$（两角及其中一角的对边对应相等的两个三角形全等），可得$\triangle DEM\cong\triangle DFN$。
根据全等三角形的对应边相等，所以$DE = DF$。

3. 如图,在$\triangle ABC$中,$AB \neq AC$,$\triangle ABC的外角\angle EAC的平分线交BC的延长线于点D$,$DE \perp BA$,交$BA的延长线于点E$,$DF \perp AC$,交$AC的延长线于点F$,连接$EF$. 求证：$EF \perp AD$.

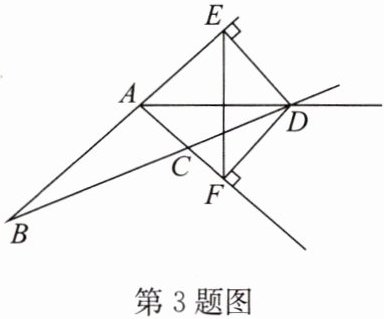
答案： 解：
因为$AD$平分$\angle EAC$，$DE\perp BA$，$DF\perp AC$，
根据角平分线的性质：角平分线上的点到角两边的距离相等，所以$DE = DF$。
在$Rt\triangle ADE$和$Rt\triangle ADF$中，
$\left\{\begin{array}{l}AD = AD\\DE = DF\end{array}\right.$（$HL$定理：斜边和一条直角边对应相等的两个直角三角形全等）
所以$Rt\triangle ADE\cong Rt\triangle ADF$，
则$AE = AF$（全等三角形对应边相等）。
又因为$AD$平分$\angle EAC$，
根据等腰三角形三线合一的性质（等腰三角形顶角的平分线，底边上的中线，底边上的高相互重合），
所以$AD\perp EF$，即$EF\perp AD$。