1. 有
两条边
相等的三角形叫作等腰三角形,相等的边叫作腰
.
答案:
两条边 腰
2. 等腰三角形的性质定理 1:等腰三角形的
两底角
相等(简称“等边对等角
”).
答案:
两底角 等边对等角
3. 等腰三角形的性质定理 2:等腰三角形
底边上的高线
、中线
及顶角平分线
重合(简称“三线合一
”).
答案:
底边上的高线 中线 顶角平分线 三线合一
4. 等腰三角形是轴对称图形,
底边的垂直平分线
是它的对称轴.
答案:
底边的垂直平分线
1. 等腰三角形的顶角是 $50^{\circ}$,则这个三角形的一个底角的度数是(
A.$65^{\circ}$
B.$40^{\circ}$
C.$50^{\circ}$
D.$80^{\circ}$
A
)A.$65^{\circ}$
B.$40^{\circ}$
C.$50^{\circ}$
D.$80^{\circ}$
答案:
A
2. 在 $\triangle ABC$ 中,$AB = AC$,$AD\perp BC$ 于点 $D$,且 $BD = 4$,则 $BC$ 的长为(
A.5
B.6
C.7
D.8
D
)A.5
B.6
C.7
D.8
答案:
D
3. 等腰三角形的一个外角是 $130^{\circ}$,则它的底角是(
A.$50^{\circ}$
B.$80^{\circ}$
C.$50^{\circ}$ 或 $80^{\circ}$
D.$50^{\circ}$ 或 $65^{\circ}$
D
)A.$50^{\circ}$
B.$80^{\circ}$
C.$50^{\circ}$ 或 $80^{\circ}$
D.$50^{\circ}$ 或 $65^{\circ}$
答案:
D
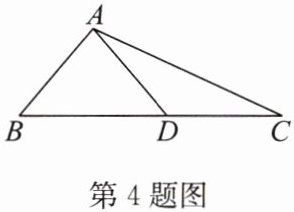
4. 如图,在 $\triangle ABC$ 中,$D$ 是 $BC$ 上一点,$\angle BAD = 80^{\circ}$,$AB = AD = DC$. 求 $\angle C$ 的度数.

答案:
1. 首先,在$\triangle ABD$中:
因为$AB = AD$,根据等腰三角形的性质“等边对等角”,设$\angle B=\angle ADB = x$。
又因为三角形内角和为$180^{\circ}$,且$\angle BAD = 80^{\circ}$,由$\angle BAD+\angle B+\angle ADB = 180^{\circ}$,可得$80^{\circ}+x + x=180^{\circ}$。
解方程$80 + 2x=180$:
移项得$2x=180 - 80$,即$2x = 100$,解得$x = 50^{\circ}$,所以$\angle ADB = 50^{\circ}$。
2. 然后,求$\angle ADC$的度数:
因为$\angle ADB+\angle ADC = 180^{\circ}$(邻补角的定义),所以$\angle ADC=180^{\circ}-\angle ADB$。
把$\angle ADB = 50^{\circ}$代入,得$\angle ADC = 130^{\circ}$。
3. 最后,在$\triangle ADC$中:
因为$AD = DC$,根据等腰三角形的性质“等边对等角”,设$\angle C=\angle DAC=y$。
又因为三角形内角和为$180^{\circ}$,即$\angle ADC+\angle C+\angle DAC = 180^{\circ}$。
把$\angle ADC = 130^{\circ}$代入$\angle ADC+\angle C+\angle DAC = 180^{\circ}$,得$130^{\circ}+y + y=180^{\circ}$。
解方程$130 + 2y=180$:
移项得$2y=180 - 130$,即$2y = 50$,解得$y = 25^{\circ}$。
所以$\angle C$的度数为$25^{\circ}$。
因为$AB = AD$,根据等腰三角形的性质“等边对等角”,设$\angle B=\angle ADB = x$。
又因为三角形内角和为$180^{\circ}$,且$\angle BAD = 80^{\circ}$,由$\angle BAD+\angle B+\angle ADB = 180^{\circ}$,可得$80^{\circ}+x + x=180^{\circ}$。
解方程$80 + 2x=180$:
移项得$2x=180 - 80$,即$2x = 100$,解得$x = 50^{\circ}$,所以$\angle ADB = 50^{\circ}$。
2. 然后,求$\angle ADC$的度数:
因为$\angle ADB+\angle ADC = 180^{\circ}$(邻补角的定义),所以$\angle ADC=180^{\circ}-\angle ADB$。
把$\angle ADB = 50^{\circ}$代入,得$\angle ADC = 130^{\circ}$。
3. 最后,在$\triangle ADC$中:
因为$AD = DC$,根据等腰三角形的性质“等边对等角”,设$\angle C=\angle DAC=y$。
又因为三角形内角和为$180^{\circ}$,即$\angle ADC+\angle C+\angle DAC = 180^{\circ}$。
把$\angle ADC = 130^{\circ}$代入$\angle ADC+\angle C+\angle DAC = 180^{\circ}$,得$130^{\circ}+y + y=180^{\circ}$。
解方程$130 + 2y=180$:
移项得$2y=180 - 130$,即$2y = 50$,解得$y = 25^{\circ}$。
所以$\angle C$的度数为$25^{\circ}$。
5. 已知一个三角形的三条边的长分别为 $n + 6$,$3n$,$n + 2$.($n$ 为正整数)
(1)若这个三角形是等腰三角形,求它的三边长;
(2)求出 $n$ 的所有整数值.
(1)若这个三角形是等腰三角形,求它的三边长;
(2)求出 $n$ 的所有整数值.
答案:
(1)①如果n+2=3n,解得n=1,三角形三边的长分别为3,3,7,不符合三角形三边关系;
②如果n+6=3n,解得n=3,三角形三边的长分别为5,9,9,符合三角形三边关系.
综上所述,等腰三角形的三边长为5,9,9.
(2)由题意,得$\begin{cases} 3n+(n+2) > n+6 \\ (n+6)+(n+2) > 3n \end{cases}$解得$\frac{4}{3}$<n<8.
∵n为整数,
∴n的所有整数值是2,3,4,5,6,7.
(1)①如果n+2=3n,解得n=1,三角形三边的长分别为3,3,7,不符合三角形三边关系;
②如果n+6=3n,解得n=3,三角形三边的长分别为5,9,9,符合三角形三边关系.
综上所述,等腰三角形的三边长为5,9,9.
(2)由题意,得$\begin{cases} 3n+(n+2) > n+6 \\ (n+6)+(n+2) > 3n \end{cases}$解得$\frac{4}{3}$<n<8.
∵n为整数,
∴n的所有整数值是2,3,4,5,6,7.
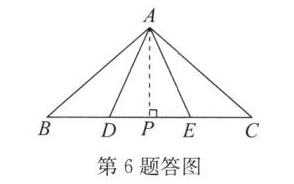
6. 如图,点 $D$,$E$ 在 $\triangle ABC$ 的边 $BC$ 上,$AB = AC$,$AD = AE$. 求证:$BD = CE$.


答案:
证明:如答图,过点A作AP⊥BC于点P.
∵AB=AC,
∴BP=PC;
∵AD=AE,
∴DP=PE,
∴BP−DP=PC−PE,
∴BD=CE.
证明:如答图,过点A作AP⊥BC于点P.

∵AB=AC,
∴BP=PC;
∵AD=AE,
∴DP=PE,
∴BP−DP=PC−PE,
∴BD=CE.
查看更多完整答案,请扫码查看


