《2025年启东中学作业本八年级数学上册苏科版连淮专版》

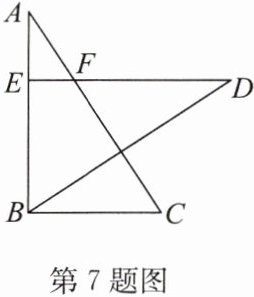
7. 如图,△ABC≌△DEB,点E在AB上,DE与AC相交于点F。
(1)当DE= 8,BC= 5时,求线段AE的长；
(2)若∠D= 35°,∠C= 60°,求∠DBC与∠AFD的度数。

答案： 解:
(1)$\because \triangle ABC\cong \triangle DEB,DE=8,BC=5,$$\therefore AB=DE=8,BE=BC=5,$$\therefore AE=AB-BE=8-5=3.$
(2)$\because \triangle ABC\cong \triangle DEB,\angle D=35^{\circ },\angle C=60^{\circ },$$\therefore \angle DBE=\angle C=60^{\circ },\angle A=\angle D=35^{\circ },\angle ABC=$$\angle DEB,$$\therefore \angle ABC=180^{\circ }-\angle A-\angle C=85^{\circ },$$\therefore \angle DBC=\angle ABC-\angle DBE=85^{\circ }-60^{\circ }=25^{\circ }.$ $\because \angle ABC=85^{\circ },\therefore \angle DEB=85^{\circ },$$\therefore \angle AED=180^{\circ }-\angle DEB=180^{\circ }-85^{\circ }=95^{\circ },$$\therefore \angle AFE=180^{\circ }-\angle A-\angle AED=50^{\circ },$$\therefore \angle AFD=180^{\circ }-\angle AFE=130^{\circ }.$

1.基本事实:两边及其夹角分别相等的两个三角形全等(简写成“边角边”或SAS).

答案： 两边及其夹角 SAS

2.符号语言:
在△ABC和△DEF中，
∵∠B=∠E，
AB=DE，
BC=EF，
∴△ABC≌△DEF(SAS)

答案： E BC=EF SAS

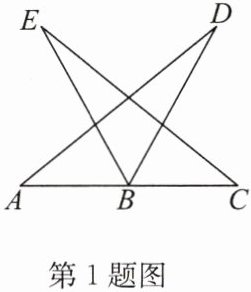
1.如图,AB= CB,DB= EB,∠ABE= ∠CBD,求证::AD= CE.

答案： 解：
因为$\angle ABE = \angle CBD$，
所以$\angle ABE+\angle EBD=\angle CBD+\angle EBD$，
即$\angle ABD = \angle CBE$。
在$\triangle ABD$和$\triangle CBE$中，
$\begin{cases}AB = CB\\\angle ABD = \angle CBE\\DB = EB\end{cases}$
根据三角形全等判定定理（SAS：两边及其夹角对应相等的三角形全等），可得$\triangle ABD\cong\triangle CBE$。
因为全等三角形的对应边相等，所以$AD = CE$。

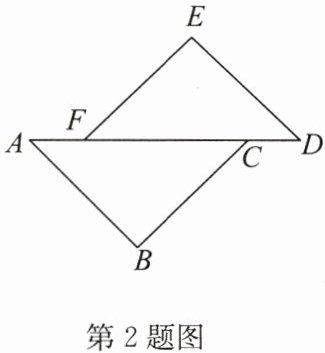
2.如图,AB//DE,AB= DE,AF= DC.求证:△ABC≌△DEF.

答案： 解：
因为$AF = DC$，
所以$AF + FC = DC + FC$，即$AC = DF$。
因为$AB// DE$，
所以$\angle A=\angle D$。
在$\triangle ABC$和$\triangle DEF$中，
$\begin{cases}AB = DE\\\angle A=\angle D\\AC = DF\end{cases}$
根据三角形全等判定定理（SAS：两边及其夹角对应相等的三角形全等），
可得$\triangle ABC\cong\triangle DEF$。