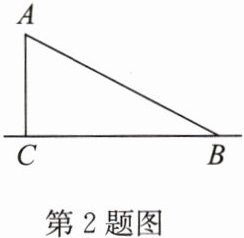
2. 如图,《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺,问折高者几何? 意思是:如图,一根竹子,原高一丈(一丈= 10 尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部 6 尺远,求折断处离地面的高度.

答案:
解:设折断处离地面的高度$AC$为$x$尺,则斜边$AB$为$(10 - x)$尺。
在$Rt\triangle ABC$中,根据勾股定理$AC^{2}+BC^{2}=AB^{2}$,可得$x^{2}+6^{2}=(10 - x)^{2}$。
展开$(10 - x)^{2}$得$x^{2}+36 = 100 - 20x+x^{2}$。
移项可得$x^{2}-x^{2}+20x = 100 - 36$。
即$20x = 64$,解得$x = 3.2$。
所以,折断处离地面的高度是$3.2$尺。
在$Rt\triangle ABC$中,根据勾股定理$AC^{2}+BC^{2}=AB^{2}$,可得$x^{2}+6^{2}=(10 - x)^{2}$。
展开$(10 - x)^{2}$得$x^{2}+36 = 100 - 20x+x^{2}$。
移项可得$x^{2}-x^{2}+20x = 100 - 36$。
即$20x = 64$,解得$x = 3.2$。
所以,折断处离地面的高度是$3.2$尺。
3. 如图,四边形 ABCD 是某校在校园一角开辟的一块四边形“试验田”,经过测量得$∠B= 90^{\circ },AB= 24m,BC= 7m,CD= 15m,AD= 20m.$
求:(1)AC 的长度和$∠D$的度数;
(2)四边形“试验田”的面积.
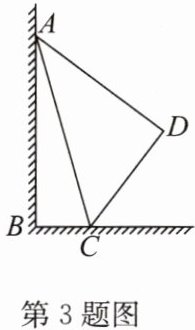
求:(1)AC 的长度和$∠D$的度数;
(2)四边形“试验田”的面积.

答案:
1. (1)
求$AC$的长度:
解:在$Rt\triangle ABC$中,$\angle B = 90^{\circ}$,根据勾股定理$AC^{2}=AB^{2}+BC^{2}$。
已知$AB = 24m$,$BC = 7m$,则$AC=\sqrt{24^{2}+7^{2}}=\sqrt{576 + 49}=\sqrt{625}=25m$。
求$\angle D$的度数:
解:在$\triangle ACD$中,$AC = 25m$,$CD = 15m$,$AD = 20m$。
因为$AD^{2}+CD^{2}=20^{2}+15^{2}=400 + 225 = 625$,$AC^{2}=25^{2}=625$。
所以$AD^{2}+CD^{2}=AC^{2}$,根据勾股定理的逆定理,$\triangle ACD$是直角三角形,且$\angle D = 90^{\circ}$。
2. (2)
求四边形“试验田”的面积:
解:四边形$ABCD$的面积$S = S_{\triangle ABC}+S_{\triangle ACD}$。
因为$S_{\triangle ABC}=\frac{1}{2}AB\cdot BC$(直角三角形面积公式$S=\frac{1}{2}ab$,$a,b$为两直角边),$S_{\triangle ACD}=\frac{1}{2}AD\cdot CD$。
已知$AB = 24m$,$BC = 7m$,$AD = 20m$,$CD = 15m$。
则$S_{\triangle ABC}=\frac{1}{2}×24×7 = 84m^{2}$,$S_{\triangle ACD}=\frac{1}{2}×20×15=150m^{2}$。
所以$S = 84 + 150=234m^{2}$。
综上,(1)$AC = 25m$,$\angle D = 90^{\circ}$;(2)四边形“试验田”的面积为$234m^{2}$。
求$AC$的长度:
解:在$Rt\triangle ABC$中,$\angle B = 90^{\circ}$,根据勾股定理$AC^{2}=AB^{2}+BC^{2}$。
已知$AB = 24m$,$BC = 7m$,则$AC=\sqrt{24^{2}+7^{2}}=\sqrt{576 + 49}=\sqrt{625}=25m$。
求$\angle D$的度数:
解:在$\triangle ACD$中,$AC = 25m$,$CD = 15m$,$AD = 20m$。
因为$AD^{2}+CD^{2}=20^{2}+15^{2}=400 + 225 = 625$,$AC^{2}=25^{2}=625$。
所以$AD^{2}+CD^{2}=AC^{2}$,根据勾股定理的逆定理,$\triangle ACD$是直角三角形,且$\angle D = 90^{\circ}$。
2. (2)
求四边形“试验田”的面积:
解:四边形$ABCD$的面积$S = S_{\triangle ABC}+S_{\triangle ACD}$。
因为$S_{\triangle ABC}=\frac{1}{2}AB\cdot BC$(直角三角形面积公式$S=\frac{1}{2}ab$,$a,b$为两直角边),$S_{\triangle ACD}=\frac{1}{2}AD\cdot CD$。
已知$AB = 24m$,$BC = 7m$,$AD = 20m$,$CD = 15m$。
则$S_{\triangle ABC}=\frac{1}{2}×24×7 = 84m^{2}$,$S_{\triangle ACD}=\frac{1}{2}×20×15=150m^{2}$。
所以$S = 84 + 150=234m^{2}$。
综上,(1)$AC = 25m$,$\angle D = 90^{\circ}$;(2)四边形“试验田”的面积为$234m^{2}$。
用勾股定理去探究一些学科内的综合问题,常需找(或构造出)
直角
三角形.
答案:
直角
1. 如图,请在数轴上画出表示$\sqrt {10}$的点 P.


答案:
1.解:如答图所示,点P即为所求.

1.解:如答图所示,点P即为所求.

2. 如图,在$△ABC$中,$AD⊥BC$,垂足为 D. 求证:$AB^{2}-AC^{2}= BD^{2}-CD^{2}.$


答案:
解:
因为$AD\perp BC$,所以$\triangle ABD$和$\triangle ACD$都是直角三角形。
根据勾股定理,在$\triangle ABD$中,$AB^{2}=AD^{2}+BD^{2}$,即$AD^{2}=AB^{2}-BD^{2}$。
在$\triangle ACD$中,$AC^{2}=AD^{2}+CD^{2}$,即$AD^{2}=AC^{2}-CD^{2}$。
所以$AB^{2}-BD^{2}=AC^{2}-CD^{2}$,移项可得$AB^{2}-AC^{2}=BD^{2}-CD^{2}$。
综上,$AB^{2}-AC^{2}=BD^{2}-CD^{2}$得证。
因为$AD\perp BC$,所以$\triangle ABD$和$\triangle ACD$都是直角三角形。
根据勾股定理,在$\triangle ABD$中,$AB^{2}=AD^{2}+BD^{2}$,即$AD^{2}=AB^{2}-BD^{2}$。
在$\triangle ACD$中,$AC^{2}=AD^{2}+CD^{2}$,即$AD^{2}=AC^{2}-CD^{2}$。
所以$AB^{2}-BD^{2}=AC^{2}-CD^{2}$,移项可得$AB^{2}-AC^{2}=BD^{2}-CD^{2}$。
综上,$AB^{2}-AC^{2}=BD^{2}-CD^{2}$得证。
查看更多完整答案,请扫码查看


