2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图,扇形AOB的圆心角$∠AOB= 90^{\circ }$,半径$OA= 6$,D是$\overset{\frown }{AB}$上一点,$AE⊥AO$交OD的延长线于点E,$BG⊥OB$交OE于点G.若$DE= 4$,则BG的长为
$\frac{9}{2}$
.
答案:
$\frac{9}{2}$
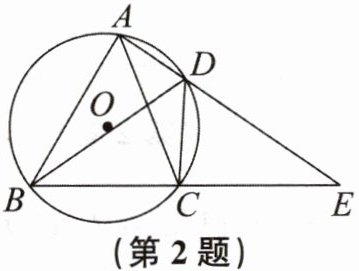
2. (2024秋·绍兴诸暨期末节选)如图,四边形ABCD内接于$\odot O$,满足$\overset{\frown }{AB}= 2\overset{\frown }{CD}$,连结AC,BD,延长BC,AD相交于点E.
(1)求证:$\triangle ABE\backsim \triangle CDE$.
(2)若$∠ABC= 60^{\circ },AD= 1,BD= 3$,求AB的长.
(1)求证:$\triangle ABE\backsim \triangle CDE$.
(2)若$∠ABC= 60^{\circ },AD= 1,BD= 3$,求AB的长.

答案:
(1)证明:
∵四边形ABCD内接于$\odot O$,
(2)$\frac{8\sqrt{7}}{7}$.
(1)证明:
∵四边形ABCD内接于$\odot O$,
$\therefore ∠BAD + ∠BCD = 180^{\circ}$,
$\because ∠BCD + ∠ECD = 180^{\circ}$,
$\therefore ∠BAD = ∠ECD$,
$\because ∠AEB = ∠CED$,
$\therefore \triangle ABE \backsim \triangle CDE$。
(2)$\frac{8\sqrt{7}}{7}$.
3. (2024·温州鹿城模拟)如图,C是以AB为直径的$\odot O$上一点,过AC的中点D作$DE⊥AB$于点E,延长DE交$\odot O$于点F,连结CF交AB于点G,连结AF,BF.
【认识图形】(1)求证:$\triangle AFD\backsim \triangle ACF$.
【探索关系】(2)①求CF与DF满足的等量关系式;
②设$\frac {CG}{FG}= x,\frac {DE}{EF}= y$,求y关于x的函数表达式.
【解决问题】(3)若$CG= 2\sqrt {2},FG= 3\sqrt {2}$,求AE的长.

【认识图形】(1)求证:$\triangle AFD\backsim \triangle ACF$.
【探索关系】(2)①求CF与DF满足的等量关系式;
②设$\frac {CG}{FG}= x,\frac {DE}{EF}= y$,求y关于x的函数表达式.
【解决问题】(3)若$CG= 2\sqrt {2},FG= 3\sqrt {2}$,求AE的长.

答案:
(1)证明:
∵AB是直径,DE⊥AB,
∴∠AFB=∠AEF=90°,
∴∠AFE+∠EFB=∠ABF+∠EFB=90°,
∴∠AFE=∠ABF,
∵∠ACF=∠ABF,
∴∠AFD=∠ACF,
∵∠FAD=∠CAF,
∴△AFD∽△ACF.
(2)①$CF=\sqrt{2}DF$. ②$y=\frac{1}{2}x$.
(3)$\frac{5\sqrt{7}}{4}$.
(1)证明:
∵AB是直径,DE⊥AB,
∴∠AFB=∠AEF=90°,
∴∠AFE+∠EFB=∠ABF+∠EFB=90°,
∴∠AFE=∠ABF,
∵∠ACF=∠ABF,
∴∠AFD=∠ACF,
∵∠FAD=∠CAF,
∴△AFD∽△ACF.
(2)①$CF=\sqrt{2}DF$. ②$y=\frac{1}{2}x$.
(3)$\frac{5\sqrt{7}}{4}$.
查看更多完整答案,请扫码查看


