2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 在$\triangle ABC$中,$a$,$b$,$c分别为\angle A$,$\angle B$,$\angle C$的对边.若$\angle B = 60^{\circ}$,则$\frac{c}{a + b} + \frac{a}{c + b}$的值为(

A.$\frac{1}{2}$
B.$\frac{\sqrt{2}}{2}$
C.1
D.$\sqrt{2}$
C
)
A.$\frac{1}{2}$
B.$\frac{\sqrt{2}}{2}$
C.1
D.$\sqrt{2}$
答案:
C
2. (2024·杭州上城模拟)如图,在$\odot O$中,将$\overparen{AB}沿弦AB$翻折,使$\overparen{AB}恰好经过圆心O$,$C是劣弧AB$上一点.已知$AE = 2$,$\tan \angle CBA = \frac{\sqrt{3}}{6}$,则$AB$的长为(
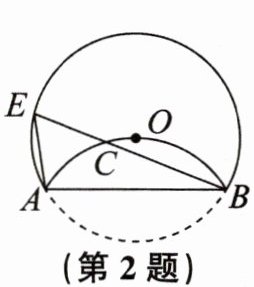
A.$2\sqrt{3}$
B.6
C.$\sqrt{39}$
D.$3\sqrt{5}$
C
)
A.$2\sqrt{3}$
B.6
C.$\sqrt{39}$
D.$3\sqrt{5}$
答案:
C
3. (2024·杭州西湖模拟)如图,在$4× 5$的网格中,每个小正方形的边长均为1.若$\triangle ABC$的顶点都在格点上,则$\sin C$的值为____
$\frac{2\sqrt{13}}{13}$
.
答案:
$\frac{2\sqrt{13}}{13}$
4. 在$\triangle ABC$中,已知$\angle A = 60^{\circ},\angle B$为锐角,且$\tan A,\cos B$恰为一元二次方程2x^{2} - 3mx + 3 = 0的两个实数根,则m =
$\sqrt{3}$
$,\triangle ABC$的形状为直角三角形
.
答案:
$\sqrt{3}$ 直角三角形
5. 进入高中以后,还会学到如下三角函数公式:$\sin (\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta$,$\cos (\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta$.例:$\sin 75^{\circ} = \sin (30^{\circ} + 45^{\circ}) = \sin 30^{\circ} \cos 45^{\circ} + \cos 30^{\circ} \sin 45^{\circ} = \frac{\sqrt{2} + \sqrt{6}}{4}$.
(1)试仿照例题,求出$\cos 75^{\circ}$的准确值.
(2)我们知道:$\tan \alpha = \frac{\sin \alpha}{\cos \alpha}$,试求出$\tan 75^{\circ}$的准确值.
(3)根据所学知识,请你巧妙地构造一个合适的直角三角形,求出$\tan 75^{\circ}$的准确值(要求分母有理化),并和(2)中的结论进行比较.
(1)试仿照例题,求出$\cos 75^{\circ}$的准确值.
(2)我们知道:$\tan \alpha = \frac{\sin \alpha}{\cos \alpha}$,试求出$\tan 75^{\circ}$的准确值.
(3)根据所学知识,请你巧妙地构造一个合适的直角三角形,求出$\tan 75^{\circ}$的准确值(要求分母有理化),并和(2)中的结论进行比较.
答案:
(1) $\frac{\sqrt{6}-\sqrt{2}}{4}$.
(2) $2+\sqrt{3}$.
(3) ,$\tan 75^{\circ}=\sqrt{3}+2$,与
(2)中求出的值相等.
(1) $\frac{\sqrt{6}-\sqrt{2}}{4}$.
(2) $2+\sqrt{3}$.
(3) ,$\tan 75^{\circ}=\sqrt{3}+2$,与
(2)中求出的值相等.
查看更多完整答案,请扫码查看


