《2025年万唯中考大小卷八年级数学下册人教版安徽专版》

21. (7分)小李在计算式子“■$\times\sqrt{\frac{7}{4}}+\sqrt{28}\div(\sqrt{7}-\frac{1}{\sqrt{7}})$”时发现“■”处的数值印刷不清.
(1)他把“■”猜成2，请你计算：$2\times\sqrt{\frac{7}{4}}+\sqrt{28}\div(\sqrt{7}-\frac{1}{\sqrt{7}})$；
(2)小李妈妈说：“你猜错了，这道题的标准答案是$\frac{5}{2}$.”请你计算原题中“■”处的数值.

答案：
解:
(1)原式$=2\times\frac{\sqrt{7}}{\sqrt{4}}+\sqrt{28}\div(\sqrt{7}-\frac{1}{\sqrt{7}})$
$=2\times\frac{\sqrt{7}}{2}+2\sqrt{7}\div(\sqrt{7}-\frac{\sqrt{7}}{7})$
$=\sqrt{7}+2\sqrt{7}\div\frac{6\sqrt{7}}{7}$
$=\sqrt{7}+2\sqrt{7}\times\frac{7}{6\sqrt{7}}$
$=\sqrt{7}+\frac{7}{3}$;…………………… (3分)
(2)设“”处是$a$,
原式$=a\times\sqrt{\frac{7}{4}}+\sqrt{28}\div(\sqrt{7}-\frac{1}{\sqrt{7}})$
$=a\times\frac{\sqrt{7}}{\sqrt{4}}+2\sqrt{7}\div(\sqrt{7}-\frac{\sqrt{7}}{7})$
$=\frac{\sqrt{7}a}{2}+2\sqrt{7}\div\frac{6\sqrt{7}}{7}=\frac{\sqrt{7}a}{2}+2\sqrt{7}\times\frac{7}{6\sqrt{7}}$
$=\frac{\sqrt{7}a}{2}+\frac{7}{3}=\frac{3\sqrt{7}a + 14}{6}$,
$\because$这道题的标准答案是$\frac{5}{2}$,
$\therefore\frac{3\sqrt{7}a + 14}{6}=\frac{5}{2}$,
$\therefore 3\sqrt{7}a + 14 = 15,\therefore 3\sqrt{7}a = 1$,解得$a=\frac{\sqrt{7}}{21}$,
答:原题中“”处的数值是$\frac{\sqrt{7}}{21}$. ………… (7分)

22. (7分)(教材P11第9题改编)“数形结合”是解决数学问题的一种重要的思想. 小王用“数形结合”思想探究求$\sqrt{2}$的近似值(精确到0.001)的过程如下，请将过程补充完整.
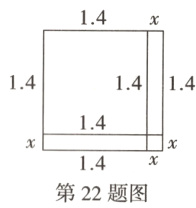
(1)先构造一个如图所示的边长为$\sqrt{2}$的正方形，已知$\sqrt{2}$介于1.4与1.5之间，设$\sqrt{2}=1.4+x$，由图可得$(\sqrt{2})^{2}=$________，即$2 = 1.96+2.8x+x^{2}$，$\because x^{2}$较小，可忽略不计，$\therefore 2.8x\approx0.04$，解得$x\approx$________，$\therefore\sqrt{2}\approx$________；
(2)已知$2.2＜\sqrt{5}＜2.3$，求$5\sqrt{5}-2\sqrt{\frac{1}{5}}-\sqrt{20}$的近似值(结果保留小数点后两位).
　

答案： 解:
(1)$(1.4 + x)^{2};0.014;1.414$; ……… (3分)
(2)原式$=5\sqrt{5}-\frac{2\sqrt{5}}{5}-2\sqrt{5}=\frac{13\sqrt{5}}{5}$,
设$(\sqrt{5})^{2}=(2.2 + x)^{2}$,
即$5 = 4.84 + 4.4x + x^{2}$,
$\because x^{2}$较小,可忽略不计,$\therefore 4.4x\approx0.16$,
解得$x\approx0.036,\therefore\sqrt{5}\approx2.236$, ………… (6分)
将$\sqrt{5}\approx2.236$代入$\frac{13\sqrt{5}}{5}$,得$\frac{13}{5}\times2.236\approx5.81$,
答:$5\sqrt{5}-2\sqrt{\frac{1}{5}}-\sqrt{20}$的近似值为$5.81$.
………………………… (7分)

23. (9分)(全国新考法·项目式学习——课题实践活动)对于两个正数$a$，$b$，$\because(\sqrt{a}-\sqrt{b})^{2}\geq0$，$\therefore a - 2\sqrt{ab}+b\geq0$，$\therefore a + b\geq2\sqrt{ab}$.
由此可得结论：对任意两个正整数$a$，$b$，都有$a + b\geq2\sqrt{ab}$.
【分析结论】(1)当$a$，$b$满足数量关系________时，不等式$a + b\geq2\sqrt{ab}$取等号；
【应用结论】(2)对于正数$x$，且$x\cdot\frac{1}{x}=1$，则有$x+\frac{1}{x}\geq2\sqrt{x\cdot\frac{1}{x}}$，即$x+\frac{1}{x}\geq2$，当$x=\frac{1}{x}$，即$x = 1$时，$x+\frac{1}{x}$取得最小值，最小值为2. 若$x＞0$，当$x$的值为多少时，$x+\frac{4}{x + 1}$有最小值？求出这个最小值；
【拓展应用】(3)为增强学生的劳动观念，让学生切身感受“谁知盘知餐，粒粒皆辛苦”，某校计划开展“劳动试验田”种植活动. 如图，八年级(1)班的劳动试验田位于一堵足够长的围墙边，同学们计划将本班的试验田用篱笆靠墙围设. 若要使该试验田的面积为$200m^{2}$，求所需篱笆的最短长度.
　　　　　　　　　　　　　　　

答案： 解:
(1)$a = b$; ……………………… (1分)
(2)由题意可得$x+\frac{4}{x + 1}=(x + 1)+\frac{4}{x + 1}-1$,
$\because x＞0,\therefore x + 1＞0$.
$\because(x + 1)+\frac{4}{x + 1}\geqslant2\sqrt{(x + 1)\cdot\frac{4}{x + 1}}$,
$\therefore(x + 1)+\frac{4}{x + 1}\geqslant4,\therefore(x + 1)+\frac{4}{x + 1}-1\geqslant3$,
$\therefore$当$x + 1=\frac{4}{x + 1}$,即$x = 1$时,$x+\frac{4}{x + 1}$有最小值,最小值为$3$;…………………… (5分)
(3)设该试验田的长为$x m$,宽为$y m$,
由题中结论$a + b\geqslant2\sqrt{ab}$,得$x + 2y\geqslant2\sqrt{x\cdot2y}$,
$\because xy = 200,\therefore x + 2y\geqslant2\sqrt{2xy}=2\sqrt{400}=40$,
$\therefore$当$x = 2y$,即$x = 20$时,$x + 2y$有最小值,最小值为$40$,
答:所需的篱笆的最短长度为$40 m$. …… (9分)