《2025年万唯中考大小卷八年级数学下册人教版安徽专版》

18. (11分)(全国新考法·项目式学习——数学与生活融合)为了对小区中心花园的植物进行更好地维护，该小区物业预备安装一个喷灌装置，为避免喷灌装置工作时，影响居民通行，物业收集了相关数据，制定暂行安装方案并进行测试.

【问题分析】(1)按此暂定方案测试，当喷灌装置工作时，是否会影响人行小路AD上的居民通行？若会，影响通行的路段有多长？若不会，请说明理由；
【问题解决】(2)若小区物业仍计划在A，C连线上安装喷灌装置，在喷灌装置工作时，不影响人行小路AD上的居民通行的情况下，应怎样修改安装方案？

答案：
解：
(1)会影响人行小路$AD$上的居民通行。如解图，过点$E$作$EF\perp AD$于点$F$，$\because \angle DAE = 30^{\circ}$，$AE = 4.8\ m$，$\therefore EF=\frac{1}{2}AE = 2.4\ m$，$\because 2.4\ m＜3\ m$，$\therefore$喷灌装置进行工作时，会影响人行小路$AD$上的居民通行；如解图，设人行小路$AD$从点$N$到点$M$的部分会被喷到水，则$EN = EM = 3\ m$，$\because EF\perp MN$，$\therefore \angle EFN = 90^{\circ}$，$FN = FM$，在$Rt\triangle EFN$中，$FN=\sqrt{EN^{2}-EF^{2}} = 1.8\ m$，$\therefore MN = 2FN = 3.6\ m$，$\therefore$当喷灌装置进行工作时，影响通行的路段长为$3.6\ m$；……(6分)
(2)如解图，若要使喷灌装置工作时不影响人行小路$AD$上的居民通行，则需$EF\geqslant3$，由
(1)可得$AE = 2EF$，$\therefore$当$EF\geqslant3\ m$时，$AE\geqslant6\ m$，$\therefore 6 - 4.8 = 1.2(m)$，$\therefore$小区物业应将喷灌安装位置沿着$AC$至少向右移$1.2\ m$。……(11分)

19. (12分)如图，在Rt△ABC中，∠ACB = 90°，AB = 5 cm，AC = 3 cm，动点P从点B出发沿射线BC以2 cm/s的速度匀速移动，设运动的时间为t s.
(1)若点P运动到BC的中点时，t的值为______；
(2)若BP = AP，求BP的长；

(3)当△ABP为直角三角形时，求t的值.

几何画板 动态演示 三角形中的动点问题

答案：
解：
(1)$1$；……(2分)
(2)若$BP = AP$，如解图①，设$BP$的长为$x\ cm$，则$AP = x\ cm$，$\because BC = 4\ cm$，$BP = x\ cm$，$\therefore CP=(4 - x)\ cm$，在$Rt\triangle ACP$中，$AP^{2}=CP^{2}+AC^{2}$，$\therefore x^{2}=(4 - x)^{2}+3^{2}$，解得$x=\frac{25}{8}$，$\therefore BP$的长为$\frac{25}{8}\ cm$；……(6分)
(3)由题意可得$BP = 2t\ cm$，分类讨论如下：①当$\angle APB$为直角时，如解图②，点$P$与点$C$重合，$BP = BC = 4\ cm$，即$2t = 4$，解得$t = 2$；……(8分)②当$\angle BAP$为直角时，如解图③，$BP = 2t\ cm$，$CP=(2t - 4)\ cm$，$AC = 3\ cm$，在$Rt\triangle ACP$中，$AP^{2}=AC^{2}+CP^{2}$，在$Rt\triangle ABP$中，$AB^{2}+AP^{2}=BP^{2}$，$\therefore AP^{2}=AC^{2}+CP^{2}=BP^{2}-AB^{2}$，即$3^{2}+(2t - 4)^{2}=(2t)^{2}-5^{2}$，解得$t=\frac{25}{8}$，综上所述，当$\triangle ABP$为直角三角形时，$t$的值为$2$或$\frac{25}{8}$。……(12分)

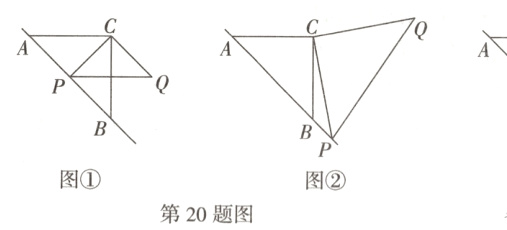
20. (14分)(全国新考法·综合与实践——操作探究)已知△ABC是等腰直角三角形，P是直线AB上一动点，连接CP，以CP为腰在直线CP的右侧作等腰直角△CPQ，∠ACB = ∠PCQ = 90°，探究并解决下列问题：
【初步尝试】(1)如图①，当CP⊥AB时，若AB = 2，则PQ的长为_______；
【探究发现】(2)如图②，若点P在AB的延长线上，请判断AP，PB和PQ之间的关系，并说明理由；
【拓展延伸】(3)当S△APC：S△BPC = 1：3，且AC = $\sqrt{10}$时，求PQ的长.

答案：
解：
(1)$\sqrt{2}$；……(2分)
(2)$AP^{2}+PB^{2}=PQ^{2}$。……(4分)理由：如解图①，连接$BQ$，$\because \triangle ABC$和$\triangle PCQ$均为等腰直角三角形，$\angle ACB=\angle PCQ = 90^{\circ}$，$\therefore AC = BC$，$PC = QC$，$\angle ABC=\angle CAB = 45^{\circ}$，$\therefore \angle ACB+\angle BCP=\angle PCQ+\angle BCP$，即$\angle ACP=\angle BCQ$，$\therefore \triangle APC\cong\triangle BQC(SAS)$，$\therefore AP = BQ$，$\angle CAP=\angle CBQ = 45^{\circ}$，$\therefore \angle ABQ=\angle ABC+\angle CBQ = 90^{\circ}$，即$AB\perp BQ$，$\therefore \angle QBP = 90^{\circ}$，$\therefore \triangle PBQ$为直角三角形，$\therefore BQ^{2}+PB^{2}=PQ^{2}$，$\therefore AP^{2}+PB^{2}=PQ^{2}$；……(6分)
(3)如解图②、解图③，过点$C$作$CD\perp AB$，垂足为点$D$，$\because S_{\triangle APC}:S_{\triangle BPC}=1:3$，$\therefore \frac{\frac{1}{2}AP\cdot CD}{\frac{1}{2}BP\cdot CD}=\frac{1}{3}$，$\therefore \frac{AP}{BP}=\frac{1}{3}$。$\because \triangle ABC$是等腰直角三角形，$\angle ACB = 90^{\circ}$，$CD\perp AB$，$\therefore AD = CD = BD$，$\angle ADC = 90^{\circ}$，$\therefore \triangle ADC$为等腰直角三角形。$\because AC=\sqrt{10}$，$\therefore$由勾股定理得，$CD=\frac{\sqrt{2}}{2}AC=\sqrt{5}$，①如解图②，当点$P$在线段$AB$上时，$AP=\frac{1}{4}AB=\frac{1}{2}CD$，$\therefore PD=\frac{1}{2}CD$，在$Rt\triangle CPD$中，由勾股定理得，$CP=\sqrt{CD^{2}+PD^{2}}=\sqrt{CD^{2}+(\frac{1}{2}CD)^{2}}=\frac{\sqrt{5}}{2}CD=\frac{5}{2}$，在$Rt\triangle PCQ$中，由勾股定理得$PQ=\frac{5\sqrt{2}}{2}$；②如解图③，当点$P$在线段$BA$的延长线上时，$PA=\frac{1}{2}AB = CD$，$\therefore PD = 2CD$，在$Rt\triangle CPD$中，由勾股定理得，$CP=\sqrt{CD^{2}+PD^{2}}=\sqrt{CD^{2}+(2CD)^{2}}=\sqrt{5}CD = 5$，在$Rt\triangle PCQ$中，由勾股定理得$PQ = 5\sqrt{2}$。综上所述，$PQ$的长为$\frac{5\sqrt{2}}{2}$或$5\sqrt{2}$。……(14分)