《2025年万唯中考大小卷八年级数学下册人教版安徽专版》

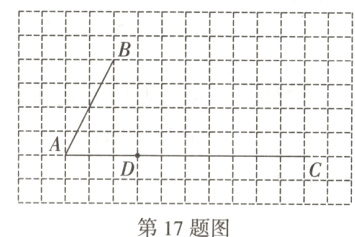
17. (安徽特色题型·网格作图题)如图，在由边长为1的小正方形组成的网格图中，点$A$，$B$，$C$，$D$均在格点(网格线的交点)上.
(1)请你在网格图中找到点$E$，画出$\square ABED$；
(2)在(1)的条件下，连接$BC$，判断$BC$与$DE$的位置关系，并说明理由.
　

答案：
解:
(1)如解图,$\square ABED$即为所求作; … (3分)
(2)$BC\perp DE$,理由如下:
连接$BC$,由解图得,$AB=\sqrt{2^{2}+4^{2}} = 2\sqrt{5}$,$BC=\sqrt{4^{2}+8^{2}} = 4\sqrt{5}$,$AC = 10$,
$\therefore AB^{2}+BC^{2}=AC^{2}$,
$\therefore\triangle ABC$是直角三角形,$\angle ABC = 90^{\circ}$,$BC\perp AB$,
由
(1)知四边形$ABED$是平行四边形,
$\therefore DE// AB,\therefore BC\perp DE$. ………………… (8分)

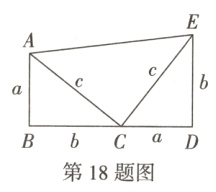
18. 勾股定理有很多种证明方法. 加菲尔德利用两个全等的直角三角形，构造了一个如图所示的图形来证明勾股定理，其中两直角边分别为$a$，$b$，斜边为$c$，且$B$，$C$，$D$三点在一条直线上. 请你利用该图形证明勾股定理，并写出证明过程.
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

答案： 证明:$\because Rt\triangle ABC\cong Rt\triangle CDE$,
$\therefore\angle BAC=\angle DCE$.
$\because\angle BAC+\angle ACB = 90^{\circ},\therefore\angle ACB+\angle DCE = 90^{\circ}$,
$\therefore\angle ACE = 180^{\circ}-90^{\circ}=90^{\circ}$,
$\therefore\triangle ACE$是一个等腰直角三角形,$S_{\triangle ACE}=\frac{1}{2}c^{2}$.
$\because S_{梯形ABDE}=\frac{1}{2}(a + b)^{2}$,且$S_{梯形ABDE}=S_{\triangle ABC}+S_{\triangle CDE}+S_{\triangle ACE}=ab+\frac{1}{2}c^{2},\therefore\frac{1}{2}(a + b)^{2}=ab+\frac{1}{2}c^{2}$,
即$a^{2}+b^{2}=c^{2}$. ………………… (8分)