2025年万唯中考大小卷八年级数学下册人教版安徽专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年万唯中考大小卷八年级数学下册人教版安徽专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
19. (10分)如图,四边形ABCD是矩形,BD是对角线,小明在矩形ABCD中用尺规作出直线MN并保留了作图痕迹,MN分别交AD,BC于点E,F,连接BE,DF.
(1)判断四边形BEDF的形状,并说明理由;
(2)若S四边形BEDF = $\frac{2}{3}$S矩形ABCD,试探究线段AD与AB之间的数量关系.
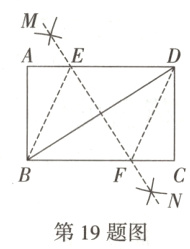
(1)判断四边形BEDF的形状,并说明理由;
(2)若S四边形BEDF = $\frac{2}{3}$S矩形ABCD,试探究线段AD与AB之间的数量关系.

答案:
解:
(1)四边形 BEDF 是菱形,理由如下:
由尺规作图可知 MN 垂直平分 BD,
∴ BE = DE,BF = DF,EF⊥BD,
∴ ∠BEF = ∠DEF.
∵ 四边形 ABCD 为矩形,
∴ AD//BC,
∴ ∠DEF = ∠BFE,
∴ ∠BEF = ∠BFE,
∴ BE = BF,
∴ BE = BF = DF = DE,
∴ 四边形 BEDF 为菱形; ……………………(5 分)
(2)
∵ S_{四边形BEDF}=$\frac{2}{3}$S_{矩形ABCD},
设 AE = x,则 DE = AD - x,
又
∵ S_{四边形BEDF}=AB·(AD - x),S_{矩形ABCD}=AB·AD,
即 AB·(AD - x)=$\frac{2}{3}$AB·AD,化简得 AD = 3x,
∴ DE = BE = AD - AE = 2x.
∵ 四边形 ABCD 是矩形,
∴ ∠A = 90°,
在 Rt△ABE 中,AB = $\sqrt{BE^{2}-AE^{2}}$=$\sqrt{(2x)^{2}-x^{2}}$=$\sqrt{3}x$,
∴ AD = $\sqrt{3}$AB. ………………………(10 分)
(1)四边形 BEDF 是菱形,理由如下:
由尺规作图可知 MN 垂直平分 BD,
∴ BE = DE,BF = DF,EF⊥BD,
∴ ∠BEF = ∠DEF.
∵ 四边形 ABCD 为矩形,
∴ AD//BC,
∴ ∠DEF = ∠BFE,
∴ ∠BEF = ∠BFE,
∴ BE = BF,
∴ BE = BF = DF = DE,
∴ 四边形 BEDF 为菱形; ……………………(5 分)
(2)
∵ S_{四边形BEDF}=$\frac{2}{3}$S_{矩形ABCD},
设 AE = x,则 DE = AD - x,
又
∵ S_{四边形BEDF}=AB·(AD - x),S_{矩形ABCD}=AB·AD,
即 AB·(AD - x)=$\frac{2}{3}$AB·AD,化简得 AD = 3x,
∴ DE = BE = AD - AE = 2x.
∵ 四边形 ABCD 是矩形,
∴ ∠A = 90°,
在 Rt△ABE 中,AB = $\sqrt{BE^{2}-AE^{2}}$=$\sqrt{(2x)^{2}-x^{2}}$=$\sqrt{3}x$,
∴ AD = $\sqrt{3}$AB. ………………………(10 分)
20. (10分)(教材P51第14题改编)如图,用硬纸板剪一个矩形ABCD,对角线AC,BD交于点O,用大头针把一根平放在矩形上的直细木条(宽度忽略不计)固定在点O处,并使细木条可以绕点O转动. 拨动细木条,使它总与AD,BC有交点. 设细木条分别交硬纸板的边AD,BC于点E,F.
(1)任选1个结论证明:①OE = OF;②AE = CF;
(2)在细木条转动过程中,当E,F恰好是AD,BC的中点时,对角线AC上有一点P,使∠EPF = 90°,若AB = 5,BC = 12,求AP的长.
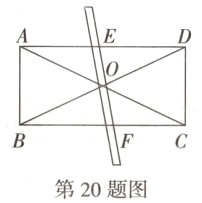
(1)任选1个结论证明:①OE = OF;②AE = CF;
(2)在细木条转动过程中,当E,F恰好是AD,BC的中点时,对角线AC上有一点P,使∠EPF = 90°,若AB = 5,BC = 12,求AP的长.

答案:
解:
(1)选择①OE = OF.
证明:
∵ 四边形 ABCD 是矩形,对角线 AC,BD 交于点 O,
∴ AO = CO,AD//BC,
∴ ∠EAO = ∠FCO,
在△AOE 和△COF 中,$\begin{cases}∠EAO = ∠FCO, \\AO = CO, \\∠AOE = ∠COF,\end{cases}$
∴ △AOE≌△COF(ASA),
∴ OE = OF;(答案不唯一) …………………(5 分)
(2)如解图,由
(1)可知,
△AOE≌△COF,
∴ OE = OF,
∵ ∠EPF = 90°,
∴ OP = $\frac{1}{2}$EF.
∵ 四边形 ABCD 是矩形,
∴ AD//BC,AD = BC,AO = CO.
∵ E,F 分别是 AD,BC 的中点,
∴ AE//BF,AE = BF,
∴ 四边形 ABFE 是平行四边形.
∵ ∠ABC = 90°,
∴ 四边形 ABFE 是矩形,
∴ EF = AB = 5,
∴ OP = $\frac{1}{2}$EF = 2.5.
在 Rt△ABC 中,AC = $\sqrt{AB^{2}+BC^{2}}$=$\sqrt{5^{2}+12^{2}}$=13,
∴ AO = CO = $\frac{1}{2}$AC = 6.5.
如解图,点 P 的位置需分情况讨论:
①当 P 在 AO 上时,AP' = AO - OP' = 6.5 - 2.5 = 4;
②当 P 在 CO 上时,AP'' = AO + OP'' = 6.5 + 2.5 = 9.
综上所述,AP 的长为 4 或 9. ……………(10 分)
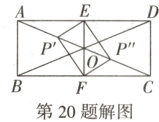
第 20 题解图
解:
(1)选择①OE = OF.
证明:
∵ 四边形 ABCD 是矩形,对角线 AC,BD 交于点 O,
∴ AO = CO,AD//BC,
∴ ∠EAO = ∠FCO,
在△AOE 和△COF 中,$\begin{cases}∠EAO = ∠FCO, \\AO = CO, \\∠AOE = ∠COF,\end{cases}$
∴ △AOE≌△COF(ASA),
∴ OE = OF;(答案不唯一) …………………(5 分)
(2)如解图,由
(1)可知,
△AOE≌△COF,
∴ OE = OF,
∵ ∠EPF = 90°,
∴ OP = $\frac{1}{2}$EF.
∵ 四边形 ABCD 是矩形,
∴ AD//BC,AD = BC,AO = CO.
∵ E,F 分别是 AD,BC 的中点,
∴ AE//BF,AE = BF,
∴ 四边形 ABFE 是平行四边形.
∵ ∠ABC = 90°,
∴ 四边形 ABFE 是矩形,
∴ EF = AB = 5,
∴ OP = $\frac{1}{2}$EF = 2.5.
在 Rt△ABC 中,AC = $\sqrt{AB^{2}+BC^{2}}$=$\sqrt{5^{2}+12^{2}}$=13,
∴ AO = CO = $\frac{1}{2}$AC = 6.5.
如解图,点 P 的位置需分情况讨论:
①当 P 在 AO 上时,AP' = AO - OP' = 6.5 - 2.5 = 4;
②当 P 在 CO 上时,AP'' = AO + OP'' = 6.5 + 2.5 = 9.
综上所述,AP 的长为 4 或 9. ……………(10 分)

第 20 题解图
21. (12分)(全国新考法·综合与实践——类比猜想)【问题情境】数学活动课上,老师提出了一个问题:如图①,在正方形ABCD中,E,F分别是边BC,CD上的点,连接AE,BF相交于点G,请同学们结合图形提出自己的猜想并证明.
小亮猜想:若AE⊥BF,则AE = BF.
(1)请帮助小亮证明他的猜想;
【类比猜想】(2)如图②,当点E,F分别在正方形ABCD的边CB,DC的延长线上时,小亮的猜想是否成立?若成立,请写出证明过程;若不成立,请说明理由;
【拓展探究】(3)如图③,将图①中线段BF向上平移后得到线段MN,此时若MN⊥AE,则MN = AE这一猜想是否成立?若成立,请写出证明过程;若不成立,请说明理由.
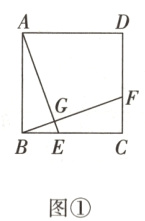
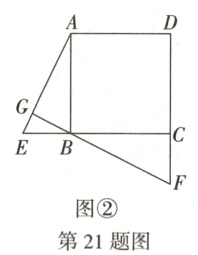
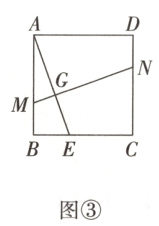
小亮猜想:若AE⊥BF,则AE = BF.
(1)请帮助小亮证明他的猜想;
【类比猜想】(2)如图②,当点E,F分别在正方形ABCD的边CB,DC的延长线上时,小亮的猜想是否成立?若成立,请写出证明过程;若不成立,请说明理由;
【拓展探究】(3)如图③,将图①中线段BF向上平移后得到线段MN,此时若MN⊥AE,则MN = AE这一猜想是否成立?若成立,请写出证明过程;若不成立,请说明理由.



答案:
(1)证明:
∵ 四边形 ABCD 是正方形,
∴ AB = BC,∠ABC = ∠BCD = 90°.
∵ AE⊥BF,
∴ ∠BGE = 90°,
∴ ∠GBE + ∠GEB = 90°.
∵ ∠BAE + ∠GEB = 90°,
∴ ∠BAE = ∠GBE.
在△ABE 和△BCF 中,$\begin{cases}∠BAE = ∠CBF, \\AB = BC, \\∠ABE = ∠BCF,\end{cases}$
∴ △ABE≌△BCF(ASA),
∴ AE = BF; …(3 分)
(2)解:成立. ………………………………(4 分)
证明如下:
∵ 四边形 ABCD 是正方形,
∴ AB = BC,∠ABE = ∠ABC = ∠BCF = 90°.
∵ AE⊥BF,
∴ ∠BGA = 90°,
∴ ∠BAE + ∠ABG = 90°.
∵ ∠CBF + ∠ABG = 90°,
∴ ∠BAE = ∠CBF,
在△ABE 和△BCF 中,
$\begin{cases}∠BAE = ∠CBF, \\AB = BC, \\∠ABE = ∠BCF,\end{cases}$
∴ △ABE≌△BCF(ASA),
∴ AE = BF; ………………………………(7 分)
(3)解:成立. ………………………………(8 分)
证明如下:如解图,过点 N 作 NK⊥AB 于点 K,
∵ 四边形 ABCD 是正方形,由题知四边形 ADNK 是矩形,
∴ AB = AD = KN,∠ABE = ∠BAD = ∠MKN = 90°,
∵ AE⊥MN,
∴ ∠AGM = 90°,
∴ ∠MAG + ∠AMG = 90°.
∵ ∠MNK + ∠AMG = 90°,
∴ ∠MNK = ∠MAG.
在△NKM 和△ABE 中,$\begin{cases}∠MNK = ∠EAB, \\NK = AB, \\∠NKM = ∠ABE,\end{cases}$
∴ △NKM≌△ABE(ASA),
∴ MN = AE. ………………………………(12 分)
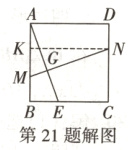
第 21 题解图
(1)证明:
∵ 四边形 ABCD 是正方形,
∴ AB = BC,∠ABC = ∠BCD = 90°.
∵ AE⊥BF,
∴ ∠BGE = 90°,
∴ ∠GBE + ∠GEB = 90°.
∵ ∠BAE + ∠GEB = 90°,
∴ ∠BAE = ∠GBE.
在△ABE 和△BCF 中,$\begin{cases}∠BAE = ∠CBF, \\AB = BC, \\∠ABE = ∠BCF,\end{cases}$
∴ △ABE≌△BCF(ASA),
∴ AE = BF; …(3 分)
(2)解:成立. ………………………………(4 分)
证明如下:
∵ 四边形 ABCD 是正方形,
∴ AB = BC,∠ABE = ∠ABC = ∠BCF = 90°.
∵ AE⊥BF,
∴ ∠BGA = 90°,
∴ ∠BAE + ∠ABG = 90°.
∵ ∠CBF + ∠ABG = 90°,
∴ ∠BAE = ∠CBF,
在△ABE 和△BCF 中,
$\begin{cases}∠BAE = ∠CBF, \\AB = BC, \\∠ABE = ∠BCF,\end{cases}$
∴ △ABE≌△BCF(ASA),
∴ AE = BF; ………………………………(7 分)
(3)解:成立. ………………………………(8 分)
证明如下:如解图,过点 N 作 NK⊥AB 于点 K,
∵ 四边形 ABCD 是正方形,由题知四边形 ADNK 是矩形,
∴ AB = AD = KN,∠ABE = ∠BAD = ∠MKN = 90°,
∵ AE⊥MN,
∴ ∠AGM = 90°,
∴ ∠MAG + ∠AMG = 90°.
∵ ∠MNK + ∠AMG = 90°,
∴ ∠MNK = ∠MAG.
在△NKM 和△ABE 中,$\begin{cases}∠MNK = ∠EAB, \\NK = AB, \\∠NKM = ∠ABE,\end{cases}$
∴ △NKM≌△ABE(ASA),
∴ MN = AE. ………………………………(12 分)

第 21 题解图
查看更多完整答案,请扫码查看


