《2025年万唯中考大小卷八年级数学下册人教版安徽专版》

20. (全国新考法·项目式学习——数学与生活融合)霍山石斛是安徽省霍山县特有的名贵中药材，也是中国国家地理标志产品. $A$村和$B$村是霍山县两个种植霍山石斛的村庄，现要在两村庄南边的公路旁修建一个霍山石斛收购点$E$. 收购点负责人对村庄及附近环境的相关数据进行测量，为收购点定点方案提供数据支持.
|
　　　　　　　　
(1)【方案确定】收购点$E$定在两个路口之间的哪个位置？
(2)【路程计算】收购人从$A$村沿小路$AB$去往$B$村收购，路程有多远？(结果保留一位小数，参考数据：$\sqrt{32.5}\approx5.70$，$\sqrt{65}\approx8.06$)

答案： 解:
(1)设$DE = x$，则$CE = 5.5 - x$，
根据题意，$BD\perp CD$，$AC\perp CD$，$BE = AE$，
$\therefore$在$Rt\triangle BDE$中，$BE^{2}=BD^{2}+DE^{2}=3.5^{2}+x^{2}$，
在$Rt\triangle ACE$中，$AE^{2}=AC^{2}+CE^{2}=2^{2}+(5.5 - x)^{2}$，
$\therefore 3.5^{2}+x^{2}=2^{2}+(5.5 - x)^{2}$，解得$x = 2$，
$\therefore DE = 2km$，$CE = 5.5 - 2 = 3.5(km)$，
$\therefore$收购点$E$在距离路口$D$向东$2km$处；
………………… (5分)
(2)$\because AE = BE$，由
(1)知$DE = CA$，$BD = EC$，
$\therefore\triangle BDE\cong\triangle ECA(SSS)$，$\therefore\angle DBE=\angle CEA$.
$\because\angle DBE+\angle BED = 90^{\circ}$，
$\therefore\angle CEA+\angle BED = 90^{\circ}$，$\therefore\angle BEA = 90^{\circ}$，
$\therefore$在$Rt\triangle BEA$中，$BE^{2}=BD^{2}+DE^{2}=3.5^{2}+2^{2}=16.25$.
$\therefore AB=\sqrt{AE^{2}+BE^{2}}\approx5.7(km)$.
$\therefore$收购人从$A$村沿小路$AB$去往$B$村收购，路程约$5.7km$. ………………… (10分)

六、（本题满分12分）
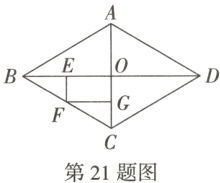
21. （教材P60第5题改编）如图，在菱形$ABCD$中，对角线$AC$，$BD$交于点$O$. $E$，$F$，$G$分别为$OB$，$BC$，$OC$的中点，连接$EF$，$FG$.
（1）求证：四边形$EFG O$是矩形；
（2）连接$DF$，已知$AD = 8$，$\angle ADC = 60^{\circ}$，求$DF$的长.
　　　　

答案：

(1)证明:$\because E,F,G$分别为$OB,BC,OC$的中点,
$\therefore EF,FG$是$\triangle OBC$的中位线,
$\therefore EF// OC,FG// OB$,
$\therefore$四边形$EFGO$是平行四边形.
$\because$四边形$ABCD$是菱形,$\therefore AC\perp BD$,
$\therefore\angle GOE = 90^{\circ}$,
$\therefore\square EFGO$是矩形; ………………… (5分)
(2)解:如解图,连接$DF$,
$\because$四边形$ABCD$是菱形,
$\therefore AD = CD,OB = OD,OA = OC,AC\perp BD$.
$\because\angle ADC = 60^{\circ},\therefore\triangle ACD$是等边三角形,
$\therefore AC = AD = 8,\therefore OC=\frac{1}{2}AC = 4$,
在$Rt\triangle COD$中,根据勾股定理,得
$OD=\sqrt{CD^{2}-OC^{2}} = 4\sqrt{3}$,
$\therefore OB = OD = 4\sqrt{3}$.
$\because E,G$分别为$OB,OC$的中点,
$\therefore OG=\frac{1}{2}OC = 2,OE=\frac{1}{2}OB = 2\sqrt{3},\therefore DE = OD+OE = 6\sqrt{3}$,
由
(1)可知,四边形$EFGO$是矩形,
$\therefore EF = OG = 2,\angle FED = 90^{\circ}$,
$\therefore DF=\sqrt{DE^{2}+EF^{2}}=\sqrt{(6\sqrt{3})^{2}+2^{2}} = 4\sqrt{7}$. ………………… (12分)