2025年万唯中考大小卷八年级数学下册人教版安徽专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年万唯中考大小卷八年级数学下册人教版安徽专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
11. 函数$y = \frac{1}{\sqrt{4x + 5}}$的自变量x的取值范围是________.
答案:
$x>-\frac{5}{4}$
12. 将直线$y = (m + 3)x + 7 - n$向下平移4个单位长度,平移后的直线与直线$y = -5x + 6$重合,则$m - n$的值为________.
答案:
-5
13. 跨学科情境 地理岩层温度 地表以下岩层的温度$T(^{\circ}C)$与所处深度$h(km)$之间存在一次函数关系. 当所处深度为2 km时,岩层的温度为90 $^{\circ}C$,当所处的深度为3 km时,岩层的温度为125 $^{\circ}C$,则所处深度为5 km时,岩层温度为________ $^{\circ}C$.
答案:
195
14. (安徽特色题型·填空双空题)如图,在平面直角坐标系中,四边形ABCD为矩形,点A的坐标为$(0,4)$,$OB = AB$,$BC:AB = 3:2$,直线l经过点$E(3,0)$,F为矩形ABCD内一点.
(1)若F为对角线AC的中点,则点F的坐标为________;
(2)若直线l与AD边交于点G,并将矩形ABCD的周长平分为相等的两部分,则点G的坐标为________.
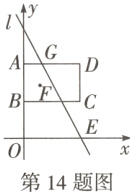
(1)若F为对角线AC的中点,则点F的坐标为________;
(2)若直线l与AD边交于点G,并将矩形ABCD的周长平分为相等的两部分,则点G的坐标为________.

答案:
(1)($\frac{3}{2}$,3);
(2)(1,4)
(1)($\frac{3}{2}$,3);
(2)(1,4)
15. (6分)已知$y = (6 + 2m)x^{2} - 5x^{|m + 2|} + 3$是关于x的一次函数.
(1)求m的值;
(2)若点$A(2,y_{1})$,$B(-1,y_{2})$,$C(5,y_{3})$均在该一次函数的图象上,试比较$y_{1}$,$y_{2}$和$y_{3}$的大小,并说明理由.
(1)求m的值;
(2)若点$A(2,y_{1})$,$B(-1,y_{2})$,$C(5,y_{3})$均在该一次函数的图象上,试比较$y_{1}$,$y_{2}$和$y_{3}$的大小,并说明理由.
答案:
解:
(1)
∵y=(6+2m)$x^{2}-5x^{|m+2|}+3$是关于x的一次函数,
∴6+2m = 0且|m + 2| = 1,
解得m = -3;(2分)
(2)$y_{2}>y_{1}>y_{3}$,(3分)
理由如下:由
(1)得m = -3,
∴一次函数解析式为y = -5x + 3.
∵-5 < 0,
∴y随x的增大而减小.
∵A(2,$y_{1}$),B(-1,$y_{2}$),C(5,$y_{3}$),-1 < 2 < 5,
∴$y_{2}>y_{1}>y_{3}$.(6分)
(1)
∵y=(6+2m)$x^{2}-5x^{|m+2|}+3$是关于x的一次函数,
∴6+2m = 0且|m + 2| = 1,
解得m = -3;(2分)
(2)$y_{2}>y_{1}>y_{3}$,(3分)
理由如下:由
(1)得m = -3,
∴一次函数解析式为y = -5x + 3.
∵-5 < 0,
∴y随x的增大而减小.
∵A(2,$y_{1}$),B(-1,$y_{2}$),C(5,$y_{3}$),-1 < 2 < 5,
∴$y_{2}>y_{1}>y_{3}$.(6分)
16. (6分)如图,已知直线$l:y = kx + b$(k为常数且k≠0)经过点$A(2,-1)$,与y轴交于点$B(0,5)$,并与直线$y = x + 2$交于点C.
(1)求直线l的解析式;
(2)求关于x,y的方程组$\begin{cases}kx + b - y = 0, \\ x - y + 2 = 0 \end{cases}$的解.
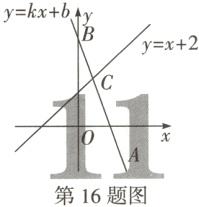
(1)求直线l的解析式;
(2)求关于x,y的方程组$\begin{cases}kx + b - y = 0, \\ x - y + 2 = 0 \end{cases}$的解.

答案:
解:
(1)
∵直线y = kx + b经过点A(2, -1),B(0,5),
将点A(2, -1),B(0,5)代入,得$\begin{cases}2k+b=-1\\b=5\end{cases}$,
解得$\begin{cases}k=-3\\b=5\end{cases}$,
∴直线l的解析式为y = -3x + 5;(3分)
(2)结合题中图象可知,方程组$\begin{cases}kx+b - y=0\\x - y+2=0\end{cases}$的解
即为直线y = kx + b与直线y = x + 2的交点C的坐标.
由
(1)知,直线l的解析式为y = -3x + 5,
∴当-3x + 5 = x + 2时,解得x = $\frac{3}{4}$,
代入直线l的解析式,求得点C的坐标为($\frac{3}{4}$,$\frac{11}{4}$),
∴关于x,y的方程组$\begin{cases}kx+b - y=0\\x - y+2=0\end{cases}$的解是$\begin{cases}x=\frac{3}{4}\\y=\frac{11}{4}\end{cases}$.(6分)
(1)
∵直线y = kx + b经过点A(2, -1),B(0,5),
将点A(2, -1),B(0,5)代入,得$\begin{cases}2k+b=-1\\b=5\end{cases}$,
解得$\begin{cases}k=-3\\b=5\end{cases}$,
∴直线l的解析式为y = -3x + 5;(3分)
(2)结合题中图象可知,方程组$\begin{cases}kx+b - y=0\\x - y+2=0\end{cases}$的解
即为直线y = kx + b与直线y = x + 2的交点C的坐标.
由
(1)知,直线l的解析式为y = -3x + 5,
∴当-3x + 5 = x + 2时,解得x = $\frac{3}{4}$,
代入直线l的解析式,求得点C的坐标为($\frac{3}{4}$,$\frac{11}{4}$),
∴关于x,y的方程组$\begin{cases}kx+b - y=0\\x - y+2=0\end{cases}$的解是$\begin{cases}x=\frac{3}{4}\\y=\frac{11}{4}\end{cases}$.(6分)
查看更多完整答案,请扫码查看


