《2025年万唯中考大小卷八年级数学下册人教版安徽专版》

14. (12分)某公司员工的月工资情况如下表：

(1)求该公司员工月工资的平均数、中位数和众数；
(2)若上月有一个员工离职，从本月开始停发该员工工资，其余员工月工资不变，但此时6名员工月工资的平均数低于原7名员工月工资的平均数，则离职的员工可能是谁？

答案： 解:
(1)该公司员工月工资的平均数$\overline{x}=\frac{1}{7}\times(9600 + 8400 + 4800 + 3000 + 2800 + 2800 + 2200)=4800$(元);
该公司员工月工资的中位数为3000元;
2800元出现了2次,出现的次数最多,
$\therefore$该公司员工月工资的众数为2800元;
……………………………………… (6分)
(2)6名员工月工资的平均数低于原7名员工月工资的平均数,说明离职员工的月工资高于原7名员工月工资的平均数,由
(1)知原7名员工月工资的平均数为4800元,月工资大于4800元的员工有经理和副经理.
$\therefore$离职的员工可能是经理或副经理. …… (12分)

15. (14分)某公司研发了甲、乙两款智能手环，为了解这两款智能手环的性能，检测部门进行了抽样调查. 在相同条件下，随机抽取甲、乙各10份样品进行了综合测评，现将测评分数(百分制)整理并绘制成如下统计图.
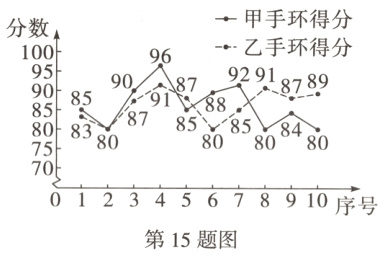
(1)分别求出甲、乙两款手环测评分数的平均数；
(2)甲、乙两款手环性能更稳定的是哪一种？请根据抽样调查的情况说明理由.

答案： 解:
(1)甲手环测评分数的平均数为$\frac{1}{10}\times(85 + 80 + 90 + 96 + 85 + 88 + 92 + 80 + 84 + 80)=86$(分);
乙手环测评分数的平均数为$\frac{1}{10}\times(83 + 80 + 87 + 91 + 87 + 80 + 85 + 91 + 87 + 89)=86$(分);……… (4分)
(2)乙手环性能更稳定,理由如下:
甲手环测评分数的方差$s_{甲}^{2}=\frac{1}{10}\times[3\times(80 - 86)^{2}+(84 - 86)^{2}+2\times(85 - 86)^{2}+(88 - 86)^{2}+(90 - 86)^{2}+(92 - 86)^{2}+(96 - 86)^{2}]=27$; ……………… (7分)
乙手环测评分数的方差$s_{乙}^{2}=\frac{1}{10}\times[2\times(80 - 86)^{2}+(83 - 86)^{2}+(85 - 86)^{2}+3\times(87 - 86)^{2}+(89 - 86)^{2}+2\times(91 - 86)^{2}]=14.4$. ………………… (10分)
$\because27＞14.4$,即$s_{甲}^{2}＞s_{乙}^{2}$,
$\therefore$乙手环的性能更稳定. …………… (14分)