《2025年名师测控七年级数学下册北师大版山西专版》

1. 计算$x(x^{2}-1)$的结果是（ ）
A. $x^{3}-1$
B. $x^{3}-x$
C. $x^{3}+x$
D. $x^{2}-x$

答案： B

2. (2024·甘肃兰州)计算$2a(a - 1)-2a^{2}$的结果是（ ）
A. $a$
B. $-a$
C. $2a$
D. $-2a$

答案： D

3. 下面四个整式中，不能表示图中阴影部分面积的是（ ）

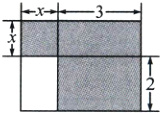
A. $x^{2}+3x + 6$
B. $x(x + 3)+6$
C. $3(x + 2)+x^{2}$
D. $x^{2}+5x$

答案： D

4. 计算：
(1)$2xy(5xy^{2}+3xy - 2)$；
(2)$(4x^{2}y - 2xy)\cdot(-3y)$；
(3)$(2ab)^{2}-4a^{2}b(b + 1)$.

答案： 解：
(1)原式$=2xy\cdot5xy^{2}+2xy\cdot3xy + 2xy\cdot(-2)=10x^{2}y^{3}+6x^{2}y^{2}-4xy$；
(2)原式$=4x^{2}y\cdot(-3y)-2xy\cdot(-3y)=-12x^{2}y^{2}+6xy^{2}$；
(3)原式$=4a^{2}b^{2}-4a^{2}b^{2}-4a^{2}b=-4a^{2}b$.

5. 计算$(a - 2)(a + 3)$的结果是（ ）
A. $a^{2}-6$
B. $a^{2}+a - 6$
C. $a^{2}+6$
D. $a^{2}-a + 6$

答案： B

6. 下列运算的结果为$x^{2}+5x - 6$的是（ ）
A. $(x + 2)(x + 3)$
B. $(x + 2)(x - 3)$
C. $(x + 6)(x - 1)$
D. $(x - 2)(x - 3)$

答案： C

7. 一个三角形的底边长为$(2a + 6b)$，高是$(3a - 5b)$，则这个三角形的面积是_______.

答案： $3a^{2}+4ab - 15b^{2}$

8. 计算：
(1)$(2x + 3)(x - 1)$；
(2)$(a + b)(a^{2}-ab + b^{2})$.

答案： 解：
(1)原式$=2x^{2}-2x + 3x - 3=2x^{2}+x - 3$；
(2)原式$=a^{3}-a^{2}b + ab^{2}+a^{2}b - ab^{2}+b^{3}=a^{3}+b^{3}$.

9. 先化简，再求值：$(x - 2y)(x + 3y)-(2x - y)(x - 4y)$，其中$x = -1$，$y = 2$.

答案： 解：原式$=x^{2}+3xy - 2xy - 6y^{2}-2x^{2}+8xy + xy - 4y^{2}=-x^{2}+10xy - 10y^{2}$. 当$x=-1$，$y = 2$时，原式$=-(-1)^{2}+10\times(-1)\times2 - 10\times2^{2}=-61$.

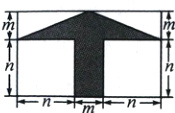
10. (2024·晋城期中)如图是某学校大门口的指示牌. 已知该指示牌是长为$(m + 2n)cm$，宽为$(m + n)cm$的长方形，左下角与右下角的空白部分是边长相等的正方形，左上角与右上角的空白部分是两个相同的直角三角形. 根据图中所标数据，解答下列问题：
(1)用含$m$，$n$的代数式表示空白部分的总面积与箭头(阴影部分)的面积；
(2)当$m = 10$，$n = 20$时，请计算箭头(阴影部分)的面积.

答案： 解：
(1)空白部分的总面积为$2n^{2}+2\times\frac{1}{2}m\times\frac{1}{2}(m + 2n)=2n^{2}+mn+\frac{1}{2}m^{2}(cm^{2})$，箭头(阴影部分)的面积为$(m + 2n)(m + n)-(2n^{2}+mn+\frac{1}{2}m^{2})=m^{2}+3mn+2n^{2}-2n^{2}-mn-\frac{1}{2}m^{2}=\frac{1}{2}m^{2}+2mn(cm^{2})$；
(2)当$m = 10$，$n = 20$时，箭头的面积为$\frac{1}{2}\times10^{2}+2\times10\times20=450(cm^{2})$.