《2025年名师测控七年级数学下册北师大版山西专版》

6.如图，已知AB//CD//EF，则x，y，z三者之间的关系是　　　　　　　　　　　　(　　　)

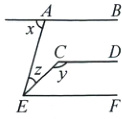
A.x + y = 180°
B.x + y - z = 180°
C.x + y + z = 360°
D.x + z = y

答案： B

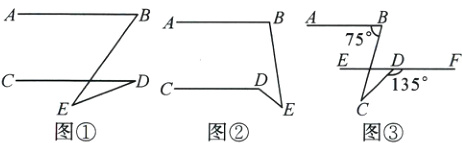
7.已知AB//CD，点E为AB，CD之外任意一点.
(1)如图①，探究∠BED与∠B，∠D之间的数量关系是________________;
(2)如图②，探究∠CDE与∠B，∠E之间的数量关系;
(3)应用:如图③，AB//EF，∠ABC = 75°，∠CDF = 135°，则∠BCD的度数为________.

答案：
解：
(1)∠B = ∠BED + ∠D
(2)∠CDE = ∠B + ∠E. 理由如下：如图②，过点E作EF//AB，则∠B + ∠BEF = 180°，所以∠DEF = ∠BEF - ∠BED = 180° - ∠B - ∠BED. 因为AB//CD，AB//EF，所以CD//EF，所以∠CDE + ∠DEF = 180°，即∠CDE + 180° - ∠B - ∠BED = 180°，所以∠CDE = ∠B + ∠BED，即∠CDE = ∠B + ∠E；
(3)30°
　　　　　　　　　　　

8.如图，AB//EF，∠B = 35°，∠E = 25°，则∠C + ∠D等于　　　　　　　　　　　　　　(　　　)
　　
A.180°　　　　　　　
　B.200°
C.240°　　　　　　　
　D.无法确定

答案： C

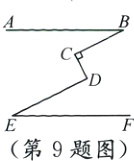
9.如图，AB//EF，∠C = 90°.探究∠B，∠CDE，∠E之间的数量关系是__________.

答案： ∠CDE + ∠B - ∠E = 90°

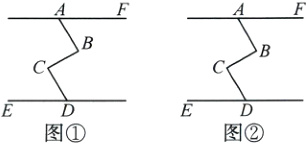
10.情境题滑雪 北京冬奥会掀起了滑雪的热潮，很多同学纷纷来到滑雪场，想亲身感受一下奥运健儿在赛场上风驰电掣的感觉.正确的滑雪姿势是上身挺直略前倾，与小腿平行，使腿的根部处于微微受力的状态，如图所示，AF//DE，AB//CD.如果人的小腿CD与地面的夹角∠CDE = 60°，你能求出身体BA与水平线的夹角∠BAF的度数吗？若能，请你用两种不同的方法求出∠BAF的度数.

答案：
解：方法一：如图①，延长AB交DE于点G. 因为AF//DE，所以∠BAF = ∠AGD. 因为AB//CD，所以∠CDE = ∠AGD. 所以∠CDE = ∠BAF. 又因为∠CDE = 60°，所以∠BAF = 60°. 方法二：如图②，过点B作BM//AF，过点C作CN//DE，则∠BAF = ∠ABM，∠CDE = ∠DCN. 因为AF//DE，BM//AF，CN//DE，所以BM//CN. 所以∠MBC = ∠BCN. 因为AB//CD，所以∠ABC = ∠BCD. 所以∠ABC - ∠MBC = ∠BCD - ∠BCN，即∠ABM = ∠DCN. 所以∠BAF = ∠CDE. 又因为∠CDE = 60°，所以∠BAF = 60°.