《2025年名师测控七年级数学下册北师大版山西专版》

一个袋中装有1个红球、5个白球、4个黑球，每个球除颜色外都相同，现从中任意摸出一个球.
（1）$P(摸到白球)=$_______，$P(摸到红球)=$_______；
（2）如果第一次摸到黑球，摸后放回，那么第二次摸到黑球的概率是_______；
（3）如果第一次摸到红球，摸后不放回，那么第二次摸到红球的概率是_______.

答案：
(1)$\frac{1}{2}$ $\frac{1}{10}$
(2)$\frac{2}{5}$
(3)0

1.（2024·湖北）在下列事件中，必然事件是　　　　　　　　　　　　　　　　(　　　)
A. 掷一次骰子，向上一面的点数是3
B. 篮球队员在罚球线上投篮一次，未投中
C. 经过有交通信号灯的路口，遇到红灯
D. 任意画一个三角形，其内角和是180°.

答案： D

2.（2024·湖南）有四枚材质、大小、背面图案完全相同的中国象棋棋子“車”“馬”“炮”“帥”，将它们背面朝上任意放置，从中随机翻开一枚，恰好翻到棋子“帥”的概率是______.

答案： $\frac{1}{4}$

3.（2024·四川泸州）在一个不透明的盒子中装有6个白球，若干个黄球，它们除颜色不同外，其余均相同. 若从中随机摸出一个球是白球的概率是$\frac{2}{3}$，则黄球的个数为______.

答案： 3

4.（2024·大同平城区校级月考）在“优秀传统文化进校园”活动中，学校计划每周二下午第三节课时间开展此项活动，拟开展活动项目为：剪纸、武术、书法、器乐，要求七年级学生人人参加，并且每人只能参加其中一项活动. 教务处在该校七年级学生中随机抽取了100名学生进行调查，并对此进行统计，绘制了如图所示的条形统计图和扇形统计图(均不完整).

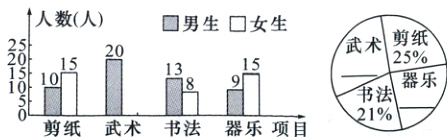
（1）请补全条形统计图和扇形统计图；
（2）在参加“剪纸”活动项目的学生中，男生所占的百分比是多少？
（3）若该校七年级学生共有500人，请估计其中参加“书法”项目活动的有多少人；
（4）学校教务处要从这些被调查的女生中随机抽取一人了解具体情况，那么正好抽到参加“器乐”活动项目的女生的概率是多少？

答案：
解：
(1)由条形图知，男生共有$10 + 20 + 13 + 9 = 52$(人)，所以女生人数为$100 - 52 = 48$(人)，所以参加武术的女生为$48 - 15 - 8 - 15 = 10$(人)，所以参加武术的人数为$20 + 10 = 30$(人)，所占百分比为$30\div100 = 30\%$. 参加器乐的人数为$9 + 15 = 24$(人)，所占百分比为$24\div100 = 24\%$. 补全条形统计图和扇形统计图如图所示；

(2)$\frac{10}{10 + 15}\times100\% = 40\%$. 答：在参加“剪纸”活动项目的学生中，男生所占的百分比为 40%；
(3)$500\times21\% = 105$(人). 答：其中参加“书法”项目活动的约有 105 人；
(4)因为女生共有 48 人，所以共有 48 种可能的结果. 因为随机抽取一人，所以每种结果出现的可能性相同. “正好抽到参加‘器乐’活动项目的女生”包含其中的 15 种结果，所以$P$(正好抽到参加“器乐”活动项目的女生)$=\frac{15}{48}=\frac{5}{16}$.