2025年名师测控七年级数学下册北师大版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名师测控七年级数学下册北师大版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1.计算:$-2x(3x^{2}y - 2xy)=$____________。
答案:
$4x^{2}y - 6x^{3}y$
2.已知$(a + b)^{2}=25,ab = 6$,则$a - b$的值为_________。
答案:
1或 -1
1.(2024·甘肃临夏州)下列各式运算结果为$a^{5}$的是( )
A. $a^{2}+a^{3}$
B. $a^{2}\cdot a^{3}$
C. $a^{10}\div a^{2}$
D. $(a^{2})^{3}$
A. $a^{2}+a^{3}$
B. $a^{2}\cdot a^{3}$
C. $a^{10}\div a^{2}$
D. $(a^{2})^{3}$
答案:
B
2.(2024·四川成都)下列计算正确的是( )
A. $(3x)^{2}=3x^{2}$
B. $3x + 3y = 6xy$
C. $(x + y)^{2}=x^{2}+y^{2}$
D. $(x + 2)(x - 2)=x^{2}-4$
A. $(3x)^{2}=3x^{2}$
B. $3x + 3y = 6xy$
C. $(x + y)^{2}=x^{2}+y^{2}$
D. $(x + 2)(x - 2)=x^{2}-4$
答案:
D
3.(2024·运城期末)生物课上,老师带领学生做实验——“制作并观察洋葱鳞片叶内表皮细胞临时装片”,所有同学经过操作,都观察到清晰的物像.科学研究表明,洋葱表皮细胞的细胞核直径大约是0.0000026m.数据“0.0000026”用科学记数法表示正确的是( )
A. $2.6\times10^{-5}$
B. $26\times10^{-5}$
C. $2.6\times10^{-6}$
D. $26\times10^{-7}$
A. $2.6\times10^{-5}$
B. $26\times10^{-5}$
C. $2.6\times10^{-6}$
D. $26\times10^{-7}$
答案:
C
4.通过计算几何图形的面积可表示一些代数恒等式,小明从图中得到的一个代数恒等式是( )

A. $x(x + y)=2x + xy$
B. $(x + y)(x + y)=x^{2}+y^{2}$
C. $(x + y)(x + 2y)=x^{2}+2y^{2}$
D. $(x + 2y)(x + y)=x^{2}+3xy + 2y^{2}$

A. $x(x + y)=2x + xy$
B. $(x + y)(x + y)=x^{2}+y^{2}$
C. $(x + y)(x + 2y)=x^{2}+2y^{2}$
D. $(x + 2y)(x + y)=x^{2}+3xy + 2y^{2}$
答案:
D
5.(2024·太原期末)先化简,再求值:$[(2x + y)(2x - y)+(x - y)^{2}]\div x$,其中$x = -2,y = 3$。
答案:
解:原式$=(4x^{2}-y^{2}+x^{2}-2xy + y^{2})\div x=(5x^{2}-2xy)\div x = 5x - 2y$. 当$x = -2$,$y = 3$时,原式$=5\times(-2)-2\times3=-16$.
6.(2024·晋城期中)综合与实践
【阅读材料】
我国著名数学家华罗庚教授曾说过:“数形结合百般好,隔裂分家万事休”.数形结合就是把抽象的数学语言、数量关系与直观的几何图形结合起来,可以使复杂、难懂的问题具体化,从而把握数学问题的本质,实现优化解题的目的.例如,教材在探究平方差与完全平方公式时,就利用了数形结合的方法.
【类比探究】
对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.如图,若将图①中的阴影部分(四个全等的小正方形)移动变换成如图②所示的图形,根据两个图形中阴影部分的关系,解答下列问题.
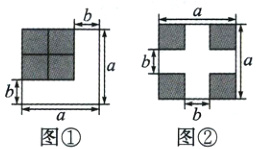
(1)写出图①所表示的数学等式:________;
【解决问题】
(2)利用(1)中得到的结论,计算:若$(6 + x)x = 7$,求$(6 + x)^{2}+x^{2}$的值;
【拓展应用】
(3)将图②阴影部分用剪刀剪去,剩下部分围成一个长方体盒子(无盖),若阴影部分的面积为$16$cm²,试求围成的长方体盒子的高.
【阅读材料】
我国著名数学家华罗庚教授曾说过:“数形结合百般好,隔裂分家万事休”.数形结合就是把抽象的数学语言、数量关系与直观的几何图形结合起来,可以使复杂、难懂的问题具体化,从而把握数学问题的本质,实现优化解题的目的.例如,教材在探究平方差与完全平方公式时,就利用了数形结合的方法.
【类比探究】
对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.如图,若将图①中的阴影部分(四个全等的小正方形)移动变换成如图②所示的图形,根据两个图形中阴影部分的关系,解答下列问题.

(1)写出图①所表示的数学等式:________;
【解决问题】
(2)利用(1)中得到的结论,计算:若$(6 + x)x = 7$,求$(6 + x)^{2}+x^{2}$的值;
【拓展应用】
(3)将图②阴影部分用剪刀剪去,剩下部分围成一个长方体盒子(无盖),若阴影部分的面积为$16$cm²,试求围成的长方体盒子的高.
答案:
解:
(1)$(a - b)^{2}=a^{2}-2ab + b^{2}$
(2)设$6 + x = a$,$x = b$,所以$a - b = 6 + x - x = 6$. 因为$(6 + x)x = 7$,所以$ab = 7$,所以$(6 + x)^{2}+x^{2}=a^{2}+b^{2}=(a - b)^{2}+2ab = 6^{2}+2\times7 = 36 + 14 = 50$,所以$(6 + x)^{2}+x^{2}$的值为50;
(3)因为阴影部分的面积为$16cm^{2}$,所以$(a - b)^{2}=16$,所以$a - b = 4$或$a - b = -4$(舍去). $\frac{a - b}{2}=\frac{4}{2}=2(cm)$,所以这个长方体盒子的高为2 cm.
(1)$(a - b)^{2}=a^{2}-2ab + b^{2}$
(2)设$6 + x = a$,$x = b$,所以$a - b = 6 + x - x = 6$. 因为$(6 + x)x = 7$,所以$ab = 7$,所以$(6 + x)^{2}+x^{2}=a^{2}+b^{2}=(a - b)^{2}+2ab = 6^{2}+2\times7 = 36 + 14 = 50$,所以$(6 + x)^{2}+x^{2}$的值为50;
(3)因为阴影部分的面积为$16cm^{2}$,所以$(a - b)^{2}=16$,所以$a - b = 4$或$a - b = -4$(舍去). $\frac{a - b}{2}=\frac{4}{2}=2(cm)$,所以这个长方体盒子的高为2 cm.
查看更多完整答案,请扫码查看


