《2025年新课程学习与检测七年级数学上册》

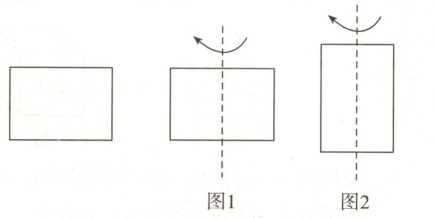
17. （10分）探究：有一个长为9cm，宽为6cm的长方形纸板，现要求以其一组对边的中点所在直线为轴，旋转$180^{\circ}$，得到一个圆柱，现可按照两种方案进行操作：
方案一：以较长的一组对边的中点所在直线为轴旋转，如图1所示；
方案二：以较短的一组对边的中点所在直线为轴旋转，如图2所示.
（1）请通过计算说明哪种方案构造的圆柱的体积大.
（2）若将此长方形绕着它其中一条边所在的直线旋转$360^{\circ}$，得到的圆柱的体积为多少？

答案：
(1)方案一构造的圆柱的体积大.
(2)486π $cm^3$或324π $cm^3$.

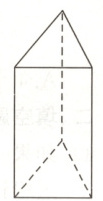
18. (6分)如图所示，这个三棱柱的高为5cm，底面是一个边长为3cm的等边三角形.
(1)该三棱柱有9条棱，有5个面.
(2)用一个平面去截该三棱柱，截面形状不可能是④⑤(填序号).
①三角形 ②长方形 ③五边形 ④六边形 ⑤圆
(3)该三棱柱的所有侧面的面积之和是45$cm^{2}$.

答案：
(1)9 5
(2)④⑤
(3)45

19. (8分)如图所示，在平整的地面上，将若干个棱长均为1cm的小正方体堆成一个几何体，并放置在墙脚.

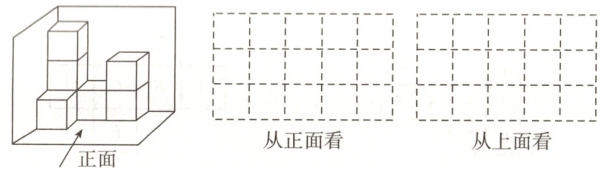
(1)请画出这个几何体从正面和上面看到的形状图.
(2)若将其露在外面的面涂上一层漆(不包括与墙和地面接触的部分)，则其涂漆面积为16$cm^{2}$.
(3)添加若干个上述小正方体后，所成几何体从左面和上面看到的形状图不变，则有5种添加方式.

答案：

(1)解：如图所示.

(2)16 解析：涂漆部分的面积为6 + 4 + 4 + 2 = 16($cm^2$).
(3)5 解析：这个几何体从左面和上面看到的形状如图所示.
　
在从上面看到的形状图中标注出相应位置增添小正方体的情况，因此有以下5种添加方式：①第1处增添1块；②第1处增添2块；③第2处增添1块；④第1处增添1块，第2处增添1块；⑤第1处增添2块，第2处增添1块.

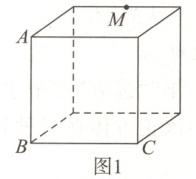
20. (10分)如图所示，图1为一个棱长为8的正方体，图2为图1的表面展开图(数字和字母写在外表面上，字母也可以表示数)，请根据要求回答问题.
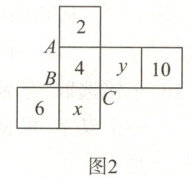
(1)如果正方体相对面上的两个数字之和相等，则$x =$12，$y =$8.
(2)如果面“10”是左面，面“6”在前面，则上面是2(选填“$x$”“$y$”或“2”).
(3)图1中，$M$为所在棱的中点，在图2中找到点$M$的位置，直接写出图2中$\triangle ABM$的面积.

答案：

(1)12 8 解析：
∵正方体相对面上的两个数字之和相等，
∴2 + x = 4 + 10，6 + y = 4 + 10，
解得x = 12，y = 8.
(2)2
(3)解：因为点M所在的棱为两个面共用，所以它的位置有两种情况.
第一种情况如图1所示.

设点M左边的顶点为D，则$S_{\triangle ABM}=\frac{1}{2}AB· DM=\frac{1}{2}×8×4 = 16$.
第二种情况如图2所示.

$S_{\triangle ABM}=\frac{1}{2}AB· AM=\frac{1}{2}×8×20 = 80$.
综上所述，$\triangle ABM$的面积为16或80.