《2025年新课程学习与检测七年级数学上册》

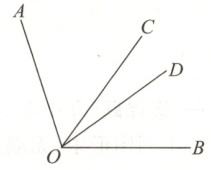
23. (5 分)如图所示,已知 $ OC $ 是 $ \angle AOB $ 的平分线,$ \angle AOD = 2\angle BOD $,$ \angle COD = 18° $,请求出 $ \angle BOD $ 的度数.

答案： 23.解:
∵OC是$\angle$AOB的平分线，
∴$\angle$BOC=$\frac{1}{2}\angle$AOB.
∵$\angle$AOD=2$\angle$BOD,
∴$\angle$AOB=3$\angle$BOD,即$\angle$BOD=$\frac{1}{3}\angle$AOB.
∴$\angle$COD=$\frac{1}{2}\angle$AOB - $\frac{1}{3}\angle$AOB=$\frac{1}{6}\angle$AOB=$18^{\circ}$.
∴$\angle$AOB=$108^{\circ}$.
∴$\angle$BOD=$\frac{1}{3}\angle$AOB=$\frac{1}{3}×108^{\circ}$=$36^{\circ}$.

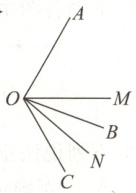
24. (8 分)(1)如图所示,已知 $ \angle AOB = 80° $,$ \angle BOC = 40° $,$ OM $ 平分 $ \angle AOC $,$ ON $ 平分 $ \angle BOC $,求 $ \angle MON $ 的度数.
(2)若(1)中 $ \angle AOB = \alpha $,其他条件不变,求 $ \angle MON $ 的大小.
(3)若(1)中 $ \angle BOC = \beta $($ \beta $ 为锐角),其他条件不变,求 $ \angle MON $ 的大小.
(4)从(1)(2)(3)的结果中总结并直接写出 $ \angle MON $ 与 $ \angle AOB $ 的关系.

答案： 24.解:
(1)
∵$\angle$AOC=$\angle$AOB+$\angle$BOC，
∴$\angle$AOC=$120^{\circ}$.
∵OM平分$\angle$AOC,
∴$\angle$MOC=$60^{\circ}$.
∵ON平分$\angle$BOC,
∴$\angle$NOC=$20^{\circ}$.
∴$\angle$MON=$60^{\circ}$ - $20^{\circ}$=$40^{\circ}$.
(2)
∵$\angle$MOC=$\frac{1}{2}(\alpha+40^{\circ})$,$\angle$NOC=$20^{\circ}$,
∴$\angle$MON=$\frac{1}{2}\alpha$.
(3)
∵$\angle$MOC=$\frac{1}{2}(80^{\circ}+\beta)$,$\angle$NOC=$\frac{1}{2}\beta$,
∴$\angle$MON=$40^{\circ}$.
(4)规律:$\angle$MON=$\frac{1}{2}\angle$AOB.

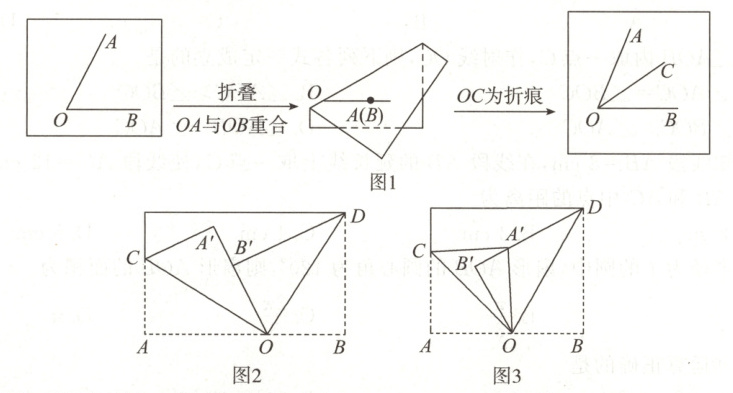
25. (7 分)利用折纸可以作出角平分线:按图 1 所示方式折叠,则 $ OC $ 为 $ \angle AOB $ 的平分线. 按图 2、图 3 所示方式折叠长方形纸片,$ OC $,$ OD $ 均是折痕,折叠后,点 $ A $ 落在点 $ A' $ 处,点 $ B $ 落在点 $ B' $ 处,连接 $ OA' $.
(1)如图 2 所示,若点 $ B' $ 恰好落在 $ OA' $ 上,且 $ \angle AOC = 32° $,则 $ \angle BOD = $$58^{\circ}$.
(2)如图 3 所示,当点 $ B' $ 在 $ \angle COA' $ 的内部时,连接 $ OB' $,若 $ \angle AOC = 44° $,$ \angle BOD = 61° $,求 $ \angle A'OB' $ 的度数.

答案： 25.
(1)$58^{\circ}$
(2)解:由题意知$\angle$AOC=$\angle A'OC$,$\angle$BOD=$\angle B'OD$.
∵$\angle$AOC+$\angle A'OC$+$\angle A'OD$+$\angle$BOD=$180^{\circ}$,$\angle$AOC=$44^{\circ}$,$\angle$BOD=$61^{\circ}$,
∴$\angle A'OD$=$180^{\circ}$ - 2$×44^{\circ}$ - $61^{\circ}$=$31^{\circ}$.
∴$\angle A'OB'$=$\angle B'OD$ - $\angle A'OD$=$30^{\circ}$.