2025年新课程学习与检测七年级数学上册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新课程学习与检测七年级数学上册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
10. $a$是不为2的有理数,我们把$\frac{2}{2 - a}$称为$a$的“哈利数”,如3的“哈利数”是$\frac{2}{2 - 3} = -2,-2$的“哈利数”是$\frac{2}{2 - (-2)} = \frac{1}{2}$.已知$a_{1} = 3,a_{2}$是$a_{1}$的“哈利数”,$a_{3}$是$a_{2}$的“哈利数”,$a_{4}$是$a_{3}$的“哈利数”$·s·s$以此类推,则$a_{2025}$的值为(
A.3
B.$-2$
C.$\frac{1}{2}$
D.$\frac{4}{3}$
A
)A.3
B.$-2$
C.$\frac{1}{2}$
D.$\frac{4}{3}$
答案:
10.A
11. 单项式$-\frac{3\pi x^{n}y}{5}$的系数是
$-\frac{3\pi}{5}$
.
答案:
11. $-\frac{3\pi}{5}$
12. 如图所示,这是一个正方体的平面展开图,将其折叠成正方体后,各相对面的数字相等,则$x + y =$
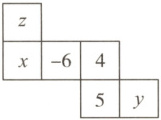
-2
.
答案:
12. -2
13. 两车同时、同地、同向出发,快车的行驶速度是$x\mathrm{km/h}$,慢车的行驶速度是$y\mathrm{km/h}$,3h后,两车之间的距离可以列式表示为
$(3x - 3y)$
$\mathrm{km}$.
答案:
13. $(3x - 3y)$
14. 如图所示,这是一种数值转换机的运算程序,若输入的数为6,则第2025次输出的数是

6
.
答案:
14. 6
15. (6分)在数轴上标出下列各数,并用“$<$”表示大小.
$-4,-2,-\frac{5}{2},0,3,3\frac{1}{2}$.
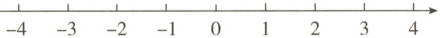
$-4,-2,-\frac{5}{2},0,3,3\frac{1}{2}$.
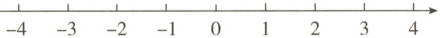
答案:
15. 解:在数轴上标出各数,如图所示.

故$-4 < -\frac{5}{2} < -2 < 0 < 3 < 3\frac{1}{2}$.
15. 解:在数轴上标出各数,如图所示.

故$-4 < -\frac{5}{2} < -2 < 0 < 3 < 3\frac{1}{2}$.
16. (16分)计算:
(1)$(-3\frac{2}{3}) - (-2.4) + (-\frac{1}{3}) - (+4\frac{2}{5})$.
(2)$(-\frac{5}{8})÷\frac{14}{3}×(-\frac{16}{5})÷(-\frac{6}{7})$.
(3)$-60×(\frac{3}{4} + \frac{5}{6} - \frac{11}{15} - \frac{7}{12})$.
(4)$-1^{2}×(1 - \frac{1}{2}) - 8÷(-2)^{2}$.
(1)$(-3\frac{2}{3}) - (-2.4) + (-\frac{1}{3}) - (+4\frac{2}{5})$.
(2)$(-\frac{5}{8})÷\frac{14}{3}×(-\frac{16}{5})÷(-\frac{6}{7})$.
(3)$-60×(\frac{3}{4} + \frac{5}{6} - \frac{11}{15} - \frac{7}{12})$.
(4)$-1^{2}×(1 - \frac{1}{2}) - 8÷(-2)^{2}$.
答案:
16. 解:
(1)原式$= (-3\frac{2}{3} - \frac{1}{3}) + (2.4 - 4.4)$
$= -4 - 2$
$= -6$.
(2)原式$= -\frac{5}{8} × \frac{3}{14} × \frac{16}{5} × \frac{7}{6} = -\frac{1}{2}$.
(3)原式$= -60 × \frac{3}{4} - 60 × \frac{5}{6} + 60 × \frac{11}{15} + 60 × \frac{7}{12}$
$= -45 - 50 + 44 + 35$
$= -(45 + 50) + (44 + 35)$
$= -95 + 79$
$= -16$.
(4)原式$= -1 × \frac{1}{2} - 8 ÷ 4$
$= -\frac{1}{2} - 2$
$= -\frac{5}{2}$.
(1)原式$= (-3\frac{2}{3} - \frac{1}{3}) + (2.4 - 4.4)$
$= -4 - 2$
$= -6$.
(2)原式$= -\frac{5}{8} × \frac{3}{14} × \frac{16}{5} × \frac{7}{6} = -\frac{1}{2}$.
(3)原式$= -60 × \frac{3}{4} - 60 × \frac{5}{6} + 60 × \frac{11}{15} + 60 × \frac{7}{12}$
$= -45 - 50 + 44 + 35$
$= -(45 + 50) + (44 + 35)$
$= -95 + 79$
$= -16$.
(4)原式$= -1 × \frac{1}{2} - 8 ÷ 4$
$= -\frac{1}{2} - 2$
$= -\frac{5}{2}$.
查看更多完整答案,请扫码查看


