2025年新课程学习与检测七年级数学上册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新课程学习与检测七年级数学上册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
24. (5分)如图所示,$C$是线段$AB$上的一个动点,点$C$从点$A$出发,以$2\ cm/s$的速度由点$A$到点$B$再到点$A$,到达点$A$时停止运动,$D$是线段$BC$的中点.已知$AB = 20\ cm$,设点$C$运动的时间为$t\ s$.
(1)求运动过程中线段$AC$的长.(用含$t$的代数式表示)
(2)在运动过程中,设$AC$的中点为$E$,线段$DE$的长度发生变化吗?若不变,直接写出$DE$的长;若发生变化,请说明理由.
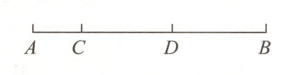
(1)求运动过程中线段$AC$的长.(用含$t$的代数式表示)
(2)在运动过程中,设$AC$的中点为$E$,线段$DE$的长度发生变化吗?若不变,直接写出$DE$的长;若发生变化,请说明理由.
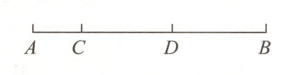
答案:
24.解:
(1)当动点C从点A向点B运动时,0≤t≤10,AC=2t;
当动点C从点B向点A运动时,10<t≤20,AC=40-2t.
(2)线段DE的长度不发生变化,且DE=10cm.
(1)当动点C从点A向点B运动时,0≤t≤10,AC=2t;
当动点C从点B向点A运动时,10<t≤20,AC=40-2t.
(2)线段DE的长度不发生变化,且DE=10cm.
25. (7分)【初步探究】
(1)如图1所示,已知线段$AB = 12\ cm$,$C$和$D$为线段$AB$上的两个动点,且$CD = 3\ cm$,$M$,$N$分别是$AC$和$BD$的中点,则$MN =$
【类比探究】
(2)已知直角$\angle COD$与平角$\angle AOB$按图2所示方式摆放在一起,且$OM$和$ON$分别是$\angle AOC$,$\angle BOD$的平分线,则$\angle MON$的度数为多少?
【知识迁移】
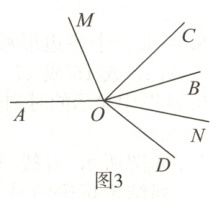
(3)当$\angle AOB = \alpha$,$\angle COD = \beta$时,将$\angle AOB$和$\angle COD$按图3所示方式摆放在一起,且$OM$和$ON$分别是$\angle AOC$,$\angle BOD$的平分线,则$\angle MON$的度数为多少?($\alpha$和$\beta$均为小于平角的角)
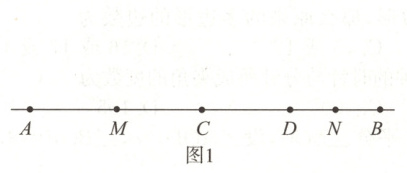
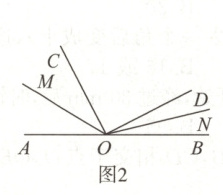
(1)如图1所示,已知线段$AB = 12\ cm$,$C$和$D$为线段$AB$上的两个动点,且$CD = 3\ cm$,$M$,$N$分别是$AC$和$BD$的中点,则$MN =$
7.5
$cm$.【类比探究】
(2)已知直角$\angle COD$与平角$\angle AOB$按图2所示方式摆放在一起,且$OM$和$ON$分别是$\angle AOC$,$\angle BOD$的平分线,则$\angle MON$的度数为多少?
【知识迁移】
(3)当$\angle AOB = \alpha$,$\angle COD = \beta$时,将$\angle AOB$和$\angle COD$按图3所示方式摆放在一起,且$OM$和$ON$分别是$\angle AOC$,$\angle BOD$的平分线,则$\angle MON$的度数为多少?($\alpha$和$\beta$均为小于平角的角)



答案:
25.
(1)7.5 解析:
∵M是AC的中点,
∴$MC=\frac{1}{2}AC.$
∵N是BD的中点,
∴$ND=\frac{1}{2}BD.$
∵AB=12cm,CD=3cm,
∴$MN=MC+CD+ND=\frac{1}{2}AC+\frac{1}{2}BD+CD=\frac{1}{2}(AC+BD)+CD=\frac{1}{2}(AB-CD)+CD=\frac{1}{2}(AB+CD)=7.5cm.$
(2)解:
∵OM是∠AOC的平分线,
∴$∠MOC=\frac{1}{2}∠AOC.$
∵ON是∠BOD的平分线,
∴$∠NOD=\frac{1}{2}∠BOD.$
∵∠COD=90°,
∴$∠MON=∠MOC+∠COD+∠NOD=\frac{1}{2}∠AOC+\frac{1}{2}∠BOD+∠COD =\frac{1}{2}(∠AOB-∠COD)+∠COD=\frac{1}{2}(∠AOB+∠COD)=135°.$
(3)解:
∵OM是∠AOC的平分线,
∴$∠MOC=\frac{1}{2}∠AOC.$
∵ON是∠BOD的平分线,
∴$∠NOD=\frac{1}{2}∠BOD.$
∵∠AOB=α,∠COD=β,
∴$∠MON=∠MOC+∠COD-∠NOD=\frac{1}{2}∠AOC-\frac{1}{2}∠BOD+∠COD =$
$\frac{1}{2}(∠AOB-∠BOC)-\frac{1}{2}(∠COD-∠BOC)+∠COD=\frac{1}{2}(∠AOB+∠COD)=$
$\frac{\alpha+\beta}{2}.$
(1)7.5 解析:
∵M是AC的中点,
∴$MC=\frac{1}{2}AC.$
∵N是BD的中点,
∴$ND=\frac{1}{2}BD.$
∵AB=12cm,CD=3cm,
∴$MN=MC+CD+ND=\frac{1}{2}AC+\frac{1}{2}BD+CD=\frac{1}{2}(AC+BD)+CD=\frac{1}{2}(AB-CD)+CD=\frac{1}{2}(AB+CD)=7.5cm.$
(2)解:
∵OM是∠AOC的平分线,
∴$∠MOC=\frac{1}{2}∠AOC.$
∵ON是∠BOD的平分线,
∴$∠NOD=\frac{1}{2}∠BOD.$
∵∠COD=90°,
∴$∠MON=∠MOC+∠COD+∠NOD=\frac{1}{2}∠AOC+\frac{1}{2}∠BOD+∠COD =\frac{1}{2}(∠AOB-∠COD)+∠COD=\frac{1}{2}(∠AOB+∠COD)=135°.$
(3)解:
∵OM是∠AOC的平分线,
∴$∠MOC=\frac{1}{2}∠AOC.$
∵ON是∠BOD的平分线,
∴$∠NOD=\frac{1}{2}∠BOD.$
∵∠AOB=α,∠COD=β,
∴$∠MON=∠MOC+∠COD-∠NOD=\frac{1}{2}∠AOC-\frac{1}{2}∠BOD+∠COD =$
$\frac{1}{2}(∠AOB-∠BOC)-\frac{1}{2}(∠COD-∠BOC)+∠COD=\frac{1}{2}(∠AOB+∠COD)=$
$\frac{\alpha+\beta}{2}.$
查看更多完整答案,请扫码查看


