第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 甲、乙两辆汽车以同样的速度同时从 $ A $ 点出发,甲汽车沿着正方形走,乙汽车沿着圆形走,(
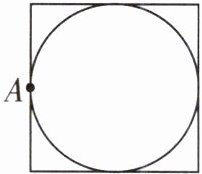
B
)先到起点。
答案:
B
2. 在一个长 $ 5 \mathrm{~cm} $、宽 $ 3 \mathrm{~cm} $ 的长方形中,剪下两个最大且相同的圆,这两个圆的周长之和是(
9.42
)$ \mathrm{cm} $。
答案:
【解析】:长方形宽为3cm,剪下最大且相同的圆,直径最大为3cm÷2=1.5cm。圆的周长=πd,一个圆周长为3.14×1.5=4.71cm,两个圆周长之和为4.71×2=9.42cm。
【答案】:9.42
【答案】:9.42
3. 填表。


答案:
| 物体名称 | 半径 | 直径 | 周长 |
|---|---|---|---|
| 盘子 | 12 cm | 24 cm | 75.36 cm |
| 花坛 | 10 m | 20 m | 62.8 m |
| 锅盖 | 3 dm | 6 dm | 18.84 dm |
|---|---|---|---|
| 盘子 | 12 cm | 24 cm | 75.36 cm |
| 花坛 | 10 m | 20 m | 62.8 m |
| 锅盖 | 3 dm | 6 dm | 18.84 dm |
1. 两根一样长的铁丝分别围成一个正方形和一个圆,(
A.圆的周长长
B.正方形的周长长
C.周长一样长
C
)。A.圆的周长长
B.正方形的周长长
C.周长一样长
答案:
C
2. 一个圆的半径扩大 $ 2 $ 倍,那么它的周长扩大(
A.$ 2 $
B.$ 4 $
C.$ 6 $
A
)倍。A.$ 2 $
B.$ 4 $
C.$ 6 $
答案:
A
1. 如右图,计算环形跑道外圈的周长。
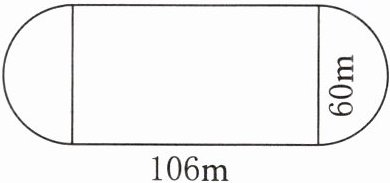

答案:
环形跑道外圈的周长由两个直道部分和两个半圆部分组成,两个半圆可拼成一个整圆。
已知直道长度为$106m$,圆的直径为$60m$。
圆的周长公式:$C = \pi d$($d$为直径)
两个直道的长度:$2×106 = 212m$
圆的周长:$3.14×60 = 188.4m$
外圈周长:$212 + 188.4 = 400.4m$
答:环形跑道外圈的周长为$400.4m$。
已知直道长度为$106m$,圆的直径为$60m$。
圆的周长公式:$C = \pi d$($d$为直径)
两个直道的长度:$2×106 = 212m$
圆的周长:$3.14×60 = 188.4m$
外圈周长:$212 + 188.4 = 400.4m$
答:环形跑道外圈的周长为$400.4m$。
2. 一辆自行车的车轮半径是 $ 40 \mathrm{~cm} $,车轮每分钟转 $ 100 $ 圈。要通过 $ 2512 \mathrm{~m} $ 的桥,大约需要几分钟?(车身的长度忽略不计)
答案:
首先,计算车轮的周长:
根据圆的周长公式:$C = 2\pi r$,
其中$r = 40 cm = 0.4 m$,$\pi$取$3.14$,
代入可得:
$C = 2 × 3.14 × 0.4 = 2.512(m)$
车轮每分钟转100圈,所以每分钟行驶的距离为:
$100 × 2.512 = 251.2(m)$,
要通过2512m的桥,所需时间为:
$2512 ÷ 251.2 = 10(分钟)$,
综上,大约需要10分钟。
根据圆的周长公式:$C = 2\pi r$,
其中$r = 40 cm = 0.4 m$,$\pi$取$3.14$,
代入可得:
$C = 2 × 3.14 × 0.4 = 2.512(m)$
车轮每分钟转100圈,所以每分钟行驶的距离为:
$100 × 2.512 = 251.2(m)$,
要通过2512m的桥,所需时间为:
$2512 ÷ 251.2 = 10(分钟)$,
综上,大约需要10分钟。
查看更多完整答案,请扫码查看


