第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 老师和同学们在操场上做游戏,学生围成一个圆圈,老师站在圆圈的中心,围成圆圈的周长是(

37.68
)m,它的面积是(113.04
)$m^2$。
答案:
围成圆圈的周长是( 37.68 )m, 它的面积是( 113.04 ) $m^2$。
2. 填表。
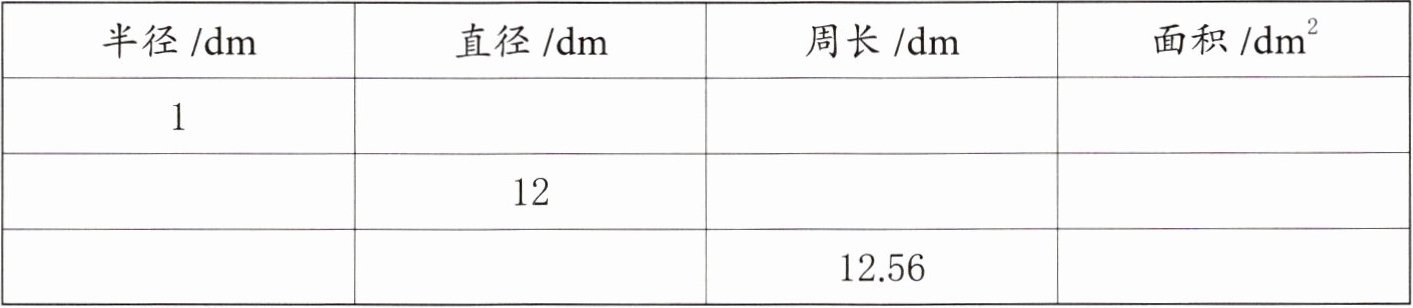

答案:
| 半径/dm | 直径/dm | 周长/dm | 面积/dm² |
| --- | --- | --- | --- |
| 1 | 2 | 6.28 | 3.14 |
| 6 | 12 | 37.68 | 113.04 |
| 2 | 4 | 12.56 | 12.56 |
| --- | --- | --- | --- |
| 1 | 2 | 6.28 | 3.14 |
| 6 | 12 | 37.68 | 113.04 |
| 2 | 4 | 12.56 | 12.56 |
3. 一个圆的半径扩大到原来的3倍,则它的面积扩大到原来的(
9
)倍。
答案:
9
二、解决问题。

(1)以(6,5)为圆心,画出由直径分别是4cm和6cm的圆组成的图形,画出该图形的一条对称轴,并求出它的面积。
(2)在方格纸上利用圆及其他已学过的平面图形,创作一幅你喜欢的图案,并对该图案的形成过程或意义进行简单介绍。

(1)以(6,5)为圆心,画出由直径分别是4cm和6cm的圆组成的图形,画出该图形的一条对称轴,并求出它的面积。
(2)在方格纸上利用圆及其他已学过的平面图形,创作一幅你喜欢的图案,并对该图案的形成过程或意义进行简单介绍。
答案:
(1)面积计算:半径$r_1$为直径的一半,即$r_1 = \frac{4}{2} = 2cm$,半径$r_2$为$r_2 = \frac{6}{2} = 3cm$。圆的面积公式为$S = \pi r^2$。两个圆的面积分别为:$S_1 = \pi × 2^2 = 4\pi$,$S_2 = \pi × 3^2 = 9\pi$,两个圆组成的图形面积为两者之和:$S = S_1 + S_2 = 4\pi + 9\pi = 13\pi$,取$\pi$的近似值为3.14,则:$S \approx 13 × 3.14 = 40.82 cm^2$,对称轴:由于两个圆同心,所以它们的对称轴是同一条经过圆心的任意直线。在这里,可以选择垂直或水平的直径作为对称轴。答案为:面积约为$40.82 cm^2$;对称轴为经过圆心(6,5)的任意直线(画图时可选择垂直或水平直径)。
(2)图案创作:在方格纸上,以(6,5)为圆心,画出半径为3cm的圆。在圆内,以圆心为中心,画出两条互相垂直的直径,将圆分为四个相等的扇形。在每个扇形内,画出一个内接等腰直角三角形,直角位于圆心,从而形成一个由四个等腰直角三角形和四个扇形组成的图案(类似风车)。图案介绍:该图案由一个圆和其内部的四个等腰直角三角形组成,通过圆的对称性和等腰直角三角形的特性,形成了一种对称且和谐的美感。这种图案可以象征平衡、和谐与无限,因为圆代表无限和完整,而等腰直角三角形则代表平衡和稳定。答案为:创作图案如上所述,图案意义为象征平衡、和谐与无限。
(1)面积计算:半径$r_1$为直径的一半,即$r_1 = \frac{4}{2} = 2cm$,半径$r_2$为$r_2 = \frac{6}{2} = 3cm$。圆的面积公式为$S = \pi r^2$。两个圆的面积分别为:$S_1 = \pi × 2^2 = 4\pi$,$S_2 = \pi × 3^2 = 9\pi$,两个圆组成的图形面积为两者之和:$S = S_1 + S_2 = 4\pi + 9\pi = 13\pi$,取$\pi$的近似值为3.14,则:$S \approx 13 × 3.14 = 40.82 cm^2$,对称轴:由于两个圆同心,所以它们的对称轴是同一条经过圆心的任意直线。在这里,可以选择垂直或水平的直径作为对称轴。答案为:面积约为$40.82 cm^2$;对称轴为经过圆心(6,5)的任意直线(画图时可选择垂直或水平直径)。
(2)图案创作:在方格纸上,以(6,5)为圆心,画出半径为3cm的圆。在圆内,以圆心为中心,画出两条互相垂直的直径,将圆分为四个相等的扇形。在每个扇形内,画出一个内接等腰直角三角形,直角位于圆心,从而形成一个由四个等腰直角三角形和四个扇形组成的图案(类似风车)。图案介绍:该图案由一个圆和其内部的四个等腰直角三角形组成,通过圆的对称性和等腰直角三角形的特性,形成了一种对称且和谐的美感。这种图案可以象征平衡、和谐与无限,因为圆代表无限和完整,而等腰直角三角形则代表平衡和稳定。答案为:创作图案如上所述,图案意义为象征平衡、和谐与无限。
查看更多完整答案,请扫码查看


