《2025年同步练习西南大学出版社五年级数学上册西师大版河南专版》

1. 商场把易拉罐饮料堆放成如下图所示的形状，你能很快算出一共有多少罐饮料吗？

答案： 观察图形可知，这堆易拉罐饮料堆成了一个近似的梯形。最上层有3罐，最下层有7罐，层数为5层。
根据梯形面积公式：总罐数 =（上层罐数 + 下层罐数）× 层数 ÷ 2
代入数据得：（3 + 7）× 5 ÷ 2 = 10 × 5 ÷ 2 = 25（罐）
答：一共有25罐饮料。

2. 有一种播种机，作业宽度是$1.5\mathrm{m}$。用拖拉机牵引，按每时行$6\mathrm{km}$计算，每时可以播种多少平方米？合多少公顷？

答案： 答题卡：
解：播种机每小时行驶距离：$6 km = 6000 m$。
播种面积计算：
面积 $A = 长 × 宽$，
$A = 6000 × 1.5 = 9000$（$ m^2$）。
单位转换：
$1 公顷 = 10000 m^2$，
$9000 m^2 = 0.9 公顷$。
答：每小时可以播种$9000$平方米，合$0.9$公顷。

3. 星星农场有一块三角形地（如下图所示），底和高都是$800\mathrm{m}$。如每台拖拉机$1$时耕地$0.8\mathrm{hm}^2$，$10$台同样的拖拉机需要几时耕完？

答案： 1. 计算三角形地的面积：
三角形面积公式$S = \frac{1}{2}×底×高$，已知底和高都是$800m$，则$S=\frac{1}{2}×800×800 = 320000m^{2}$。
因为$1hm^{2}=10000m^{2}$，所以$320000m^{2}=320000÷10000 = 32hm^{2}$。
2. 计算$10$台拖拉机$1$小时的耕地量：
已知每台拖拉机$1$时耕地$0.8hm^{2}$，则$10$台拖拉机$1$小时耕地$0.8×10 = 8hm^{2}$。
3. 计算耕完地所需时间：
总面积为$32hm^{2}$，$10$台拖拉机$1$小时耕地$8hm^{2}$，则耕完地需要的时间为$32÷8 = 4$（小时）。
答：$10$台同样的拖拉机需要$4$小时耕完。

4. 某班墙报的形状是一个梯形，上底$2\mathrm{m}$，下底$4\mathrm{m}$，高$2\mathrm{m}$。如果刊头占$0.4\mathrm{m}^2$，剩下的面积还有多大？

答案： 答题卡：
解：梯形面积公式为$S =(a + b)h÷2$（其中$a$为上底，$b$为下底，$h$为高）。
把$a = 2m$，$b = 4m$，$h = 2m$代入公式可得：
$S=(2 + 4)×2÷2$
$=6×2÷2$
$= 6m^{2}$
因为刊头占$0.4m^{2}$，所以剩下的面积为：
$6 - 0.4 = 5.6m^{2}$
答：剩下的面积是$5.6m^{2}$。

5. 洋洋准备用长$1\mathrm{m}$，宽$0.6\mathrm{m}$的长方形卡纸做三角形学具，学具的规格如下图所示。如果不计材料的损耗，洋洋最多能做多少个学具？

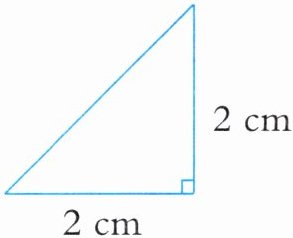
答案： 1. 单位换算：1m=100cm，0.6m=60cm。
2. 计算长方形卡纸长、宽方向可容纳的2cm长度数量：长方向：100÷2=50（个），宽方向：60÷2=30（个）。
3. 计算可剪出的边长2cm正方形个数：50×30=1500（个）。
4. 每个正方形可分成2个直角三角形学具，故三角形学具个数：1500×2=3000（个）。
结论：3000个。

6. 洋洋把妈妈买回的苹果堆放成一定的形状，使最前面一排有$4$个苹果，以后每一排比上一排多$4$个苹果，这样一共堆放了$4$排。一共有多少个苹果？

答案： 已知最前面一排有4个苹果，以后每一排比上一排多4个苹果，共堆放了4排。
第1排：4个
第2排：4 + 4 = 8个
第3排：8 + 4 = 12个
第4排：12 + 4 = 16个
总苹果数 = 4 + 8 + 12 + 16
= (4 + 16) + (8 + 12)
= 20 + 20
= 40
答：一共有40个苹果。