《2025年同步练习西南大学出版社五年级数学上册西师大版河南专版》

1. 一块平行四边形地的底是46m，高是29m。这块地的面积是多少平方米？

答案： 平行四边形面积公式：$S = a × h$（其中$S$表示面积，$a$表示底，$h$表示高）。
已知底$a = 46m$，高$h = 29m$，则面积$S = 46 × 29 = 1334$（平方米）。
答：这块地的面积是1334平方米。

2. 有一堆饮料，堆成下图的形状。最上层有4瓶，最下层有10瓶，每相邻两层相差1瓶。这堆饮料共有多少瓶？

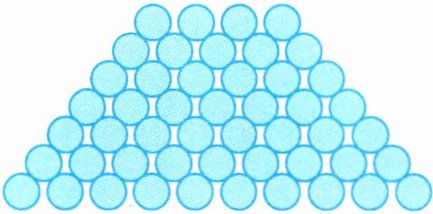
答案： 1. 确定层数：
最上层有$4$瓶，最下层有$10$瓶，每相邻两层相差$1$瓶。
层数为$10 - 4+1 = 7$（层）。
2. 计算总瓶数：
根据梯形面积公式$S=(a + b)h÷2$（这里$a$表示最上层瓶数，$b$表示最下层瓶数，$h$表示层数）。
则总瓶数为$(4 + 10)×7÷2$
$=14×7÷2$
$=49$（瓶）
答：这堆饮料共有$49$瓶。

3. 芳芳步测了学校花坛的周长(如图)，芳芳每步大约长0.6m。这个花坛的面积大约有多少平方米？

答案： 1. 计算花坛各边实际长度：
30步×0.6m/步=18m，
40步×0.6m/步=24m，
50步×0.6m/步=30m。
2. 判断花坛形状：
因18²+24²=324+576=900=30²，故为直角三角形，直角边18m、24m。
3. 计算面积：
S=18×24÷2=216m²。
答：这个花坛的面积大约有216平方米。

4. 木材加工厂堆放原木(堆放方式如下图所示)，每上一层都比原来一层少4根。已知最上层有4根，最下层有20根。
(1)这堆原木堆放了多少层？

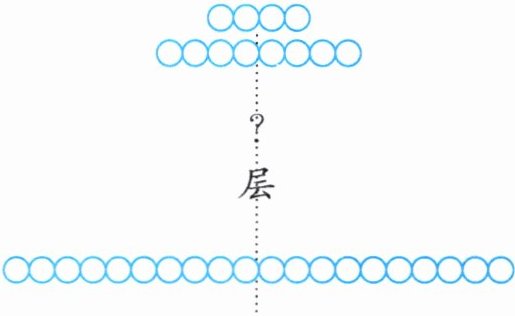
(2)一共有多少根原木？

答案：
(1) 层数：(20 - 4) ÷ 4 + 1 = 5（层）
(2) 总根数：(4 + 20) × 5 ÷ 2 = 60（根）

5. 最多可以做多少条这样的围巾？

答案： 1. 正方形彩布面积：6×6=36（平方米）
2. 一条三角形围巾面积：0.6×0.4÷2=0.12（平方米）
3. 两个三角形拼成平行四边形面积：0.6×0.4=0.24（平方米）
4. 正方形边长容纳平行四边形个数：
沿0.6米方向：6÷0.6=10（个）；沿0.4米方向：6÷0.4=15（个）
5. 平行四边形总数：10×15=150（个）
6. 三角形围巾总数：150×2=300（条）
答：最多可以做300条这样的围巾。