《2025年同步练习西南大学出版社五年级数学上册西师大版河南专版》

1. 先测量下面各图形的底和高，再分别计算出它们的面积。(精确到毫米。)

底() 底()
高() 高()
面积() 面积()

答案： 左图:
底: 40毫米。
高: 34毫米。
面积: $ \frac{1}{2} × 40 × 34 = 680 $ (平方毫米)。
右图:
底: 32毫米。
高: 15毫米。
面积: $ \frac{1}{2} × 32 × 15 = 240 $ (平方毫米)。

2. 填一填。
(1)两个完全一样的三角形可以拼成一个()形，拼成的()形的底是原三角形的底，拼成的()形的高是原三角形的高，所以三角形的面积=()×()÷()。
(2)一个平行四边形的面积是 $ 64 \, m^2 $，与它等底等高的三角形的面积是()$ m^2 $。

答案：
(1)平行四边；平行四边；平行四边；底；高；2；
(2)32

3. 一块平行四边形菜地的高是 $ 26 \, m $，底是高的 $ 3 $ 倍。这块菜地的面积是多少平方米？

答案： 答题卡作答：
底：$26 × 3 = 78(m)$。
面积：$S = ah = 78 × 26 = 2028(m^{2})$。
结论：这块菜地的面积是$2028$平方米。

4. 一块三角形的玻璃，它的底是 $ 12 \, dm $，高是 $ 6.6 \, dm $，每平方米玻璃的价钱是 $ 65 $ 元。买这块玻璃要用多少元？

答案： 1. 三角形面积公式：$ S = \frac{1}{2}ah $
2. 底 $ a = 12 \, dm = 1.2 \, m $，高 $ h = 6.6 \, dm = 0.66 \, m $
3. 面积 $ S = \frac{1}{2} × 1.2 × 0.66 = 0.396 \, m^2 $
4. 总价：$ 0.396 × 65 = 25.74 \, 元 $
答：买这块玻璃要用25.74元。

5. 有一个近似三角形的水池，底是 $ 25.5 \, m $，高是 $ 12 \, m $。这个水池占地面积有多大？

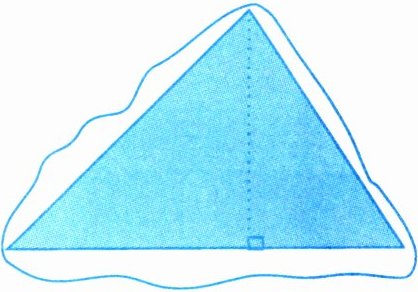
答案： 三角形面积公式：$S = \frac{1}{2}ah$（其中$a$为底，$h$为高）。
已知底$a = 25.5 \, m$，高$h = 12 \, m$，代入公式得：
$S = \frac{1}{2} × 25.5 × 12$
$= 12.75 × 12$
$= 153 \, (m^2)$
答：这个水池占地面积是$153 \, m^2$。

6. 把一个等边三角形分成 $ 4 $ 个面积相等的三角形。可以怎样分？你能想出几种方法？

答案： 方法一：连接等边三角形的一条中线，将其分成2个面积相等的小三角形，再分别在这2个小三角形中画一条中线（连接顶点与对边中点），得到4个面积相等的三角形。
方法二：将等边三角形的任意一条边四等分，连接该边所对的顶点与三个等分点，得到4个面积相等的三角形。
方法三：找到等边三角形三条边的中点，依次连接这三个中点，形成4个面积相等的小等边三角形。
结论：共3种方法。