《2025年数学学习与巩固六年级上册人教版》

4. 六(1)班12名同学分成6个小队进行乒乓球双打比赛,每两个小队之间都要赛一场,一共要赛多少场？已知第一小队已赛了5场,第二小队已赛了4场,第三小队已赛了3场,第四小队已赛了2场,第五小队已赛了1场。第六小队赛了几场？分别和哪个小队赛的？

答案： 6×(6-1)÷2=15(场)
第一小队：二、三、四、五、六，共5场
第五小队：一，共1场
第二小队：一、三、四、六，共4场
第四小队：一、二，共2场
第三小队：一、二、六，共3场
第六小队：一、二、三，共3场
答：一共要赛15场，第六小队赛了3场，分别是和第一、二、三小队赛的

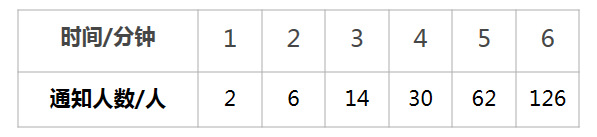
5. 某消防联队一共有126人,为保持联络方便,设计了这样一种联络方式：一旦有险情,由指导员通知两名队员,这两名队员再分别通知两名队员,以此类推。假定每同时通知两名队员需要1分钟,6分钟能通知到所有的队员吗？用列表或画图的方法找出规律,求出结果。

答案：
第1分钟，2名队员
第2分钟，2+2×2=6(名)
第3分钟，6×2+2=14(名)
第4分钟，14×2+2=30(名)
第5分钟，30×2+2=62(名)
第6分钟，62×2+2=126(名)

答：6分钟能通知到所有的队员。

6. 观察下图,最上面一层有1个小正方形,每往下一层增加2个小正方形。按这样的规律,从上往下数第5层有多少个小正方形？前10层一共有多少个小正方形？

答案： 第5层：1+2+2+2+2=9(个)
第10层:1+(10-1)×2=19(个)
1+3+5+7+9+…+19=100(个)
答：从上往下数第5层有9个小正方形。前10层一共
有100个小正方形。

$\frac{1}{1 × 2} = 1 - \frac{1}{2}$ $\frac{1}{2 × 3} = \frac{1}{2} - \frac{1}{3}$
$\frac{1}{3 × 4} = $$\frac{1}{3}$$- $$\frac{1}{4}$$\frac{1}{4 × 5} = $$\frac{1}{4}$$- $$\frac{1}{5}$
......
根据以上规律,计算下面的算式。
$\frac{1}{1 × 2} + \frac{1}{2 × 3} + \frac{1}{3 × 4} + \frac{1}{4 × 5} + … + \frac{1}{99 × 100}$
$=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+…+\frac{1}{99}-\frac{1}{100}$
$ =1-\frac{1}{100}$
$ =\frac{99}{100}$

答案： $\frac13$
$\frac14$
$\frac14$
$\frac15$
$=1-\frac12+\frac12-\frac13+\frac13-\frac14+\frac14-\frac15+…+\frac1{99}-\frac1{100}$
$ =1-\frac1{100}$
$ =\frac{99}{100}$