第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
7. 已知点 $A$,$B$ 在数轴上分别表示有理数 $a$,$b$,则 $A$,$B$ 两点之间的距离表示为 $|AB| = |a - b|$。
(1)数轴上表示数 $x$ 和 $5$ 的两点之间的距离是
(2)当 $|x + 1| = 2$ 时,$x$ 的值为
(3)当 $|x - 1| + |x + 3| = 8$ 时,$x$ 的值为
(4)当代数式 $|x - 1| + |x + 3|$ 取最小值时,相应的 $x$ 的取值范围是
(1)数轴上表示数 $x$ 和 $5$ 的两点之间的距离是
$|x - 5|$
;(用含 $x$ 的式子表示)(2)当 $|x + 1| = 2$ 时,$x$ 的值为
$1$或$-3$
;(3)当 $|x - 1| + |x + 3| = 8$ 时,$x$ 的值为
$3$或$-5$
;(4)当代数式 $|x - 1| + |x + 3|$ 取最小值时,相应的 $x$ 的取值范围是
$-3 \leq x \leq 1$
,该最小值是$4$
。
答案:
(1)$|x - 5|$
(2)
由$|x + 1| = 2$,
得$x + 1 = 2$或$x + 1 = -2$,
解得$x = 1$或$x = -3$。
故答案为:$1$或$-3$;
(3)
当$x \gt 1$时,
$x - 1 + x + 3 = 8$,
解得$x = 3$;
当$x \lt -3$时,
$1 - x - x - 3 = 8$,
解得$x = -5$;
当$-3\leq x\leq1$时,
$1 - x + x + 3 = 4 \neq 8$,无解;
综上,$x$的值为$3$或$-5$。
(4)
当$x \gt 1$时,
$|x - 1| + |x + 3|$
$= x - 1 + x + 3$
$= 2x + 2$
此时最小值大于$4$;
当$x \lt -3$时,
$|x - 1| + |x + 3|$
$= 1 - x - x - 3$
$= -2x - 2$
此时最小值大于$4$;
当$-3\leq x\leq1$时,
$|x - 1| + |x + 3|$
$= 1 - x + x + 3$
$= 4$
综上,当$-3\leq x\leq1$时,代数式取得最小值,最小值为$4$。
故答案为:$-3 \leq x \leq 1$;$4$。
(1)$|x - 5|$
(2)
由$|x + 1| = 2$,
得$x + 1 = 2$或$x + 1 = -2$,
解得$x = 1$或$x = -3$。
故答案为:$1$或$-3$;
(3)
当$x \gt 1$时,
$x - 1 + x + 3 = 8$,
解得$x = 3$;
当$x \lt -3$时,
$1 - x - x - 3 = 8$,
解得$x = -5$;
当$-3\leq x\leq1$时,
$1 - x + x + 3 = 4 \neq 8$,无解;
综上,$x$的值为$3$或$-5$。
(4)
当$x \gt 1$时,
$|x - 1| + |x + 3|$
$= x - 1 + x + 3$
$= 2x + 2$
此时最小值大于$4$;
当$x \lt -3$时,
$|x - 1| + |x + 3|$
$= 1 - x - x - 3$
$= -2x - 2$
此时最小值大于$4$;
当$-3\leq x\leq1$时,
$|x - 1| + |x + 3|$
$= 1 - x + x + 3$
$= 4$
综上,当$-3\leq x\leq1$时,代数式取得最小值,最小值为$4$。
故答案为:$-3 \leq x \leq 1$;$4$。
比较大小:(1)正数大于 0,0 大于
负数
,正数大于负数;(2)两个负数,绝对值大的反而小
;(3)数轴上左边的数小于
右边的数。
答案:
(1)负数;
(2)反而小;
(3)小于
(1)负数;
(2)反而小;
(3)小于
填空 比较大小:$-\frac{2}{3}$
<
$\frac{1}{3}$;$-\frac{7}{9}$<
$-\frac{5}{9}$。
答案:
$<$,$<$
例 1 比较大小:
$0$
名师导引 比较有理数的大小时,先化简,再观察数的符号,最后用数轴法或绝对值法比较大小。
变式训练 比较大小:
$3$
$0$
>
$-3$;$-2\frac{1}{2}$<
$-|-2\frac{1}{3}|$;$-2$>
$-5$;$-(-4)$>
$-(+5)$;名师导引 比较有理数的大小时,先化简,再观察数的符号,最后用数轴法或绝对值法比较大小。
变式训练 比较大小:
$3$
>
$|-2|$;$-|-2.3|$<
$-(-3.7)$;$-\frac{4}{5}$<
$-\frac{2}{3}$;$-\frac{6}{5}$>
$-1.5$。
答案:
>;<;<;>
例 2 有理数$m$,$n$在数轴上的对应点如图所示。
(1)在数轴上分别表示出数$-n$,$|m|$;
(2)把$m$,$n$,$-n$,$|m|$这四个数按从小到大的顺序排列,并用“<”号连接。
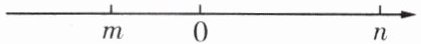
名师导引 数轴上右边的数总比左边的数大,利用数形结合比较数的大小,更形象、直观。比较几个字母所代表的数的大小时,常用数轴法。
变式训练 有理数$a$,$b$在数轴上的位置如图所示,则下列选项正确的是(

A. $a>b$
B. $|a|>|b|$
C. $-a>b$
D. $a>-b$
(1) -n在原点左侧,与n关于原点对称;|m|在原点右侧,与m关于原点对称。
(2) -n < m < |m| < n。
(1)在数轴上分别表示出数$-n$,$|m|$;
(2)把$m$,$n$,$-n$,$|m|$这四个数按从小到大的顺序排列,并用“<”号连接。
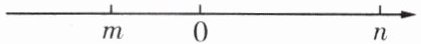
名师导引 数轴上右边的数总比左边的数大,利用数形结合比较数的大小,更形象、直观。比较几个字母所代表的数的大小时,常用数轴法。
变式训练 有理数$a$,$b$在数轴上的位置如图所示,则下列选项正确的是(
D
)
A. $a>b$
B. $|a|>|b|$
C. $-a>b$
D. $a>-b$
(1) -n在原点左侧,与n关于原点对称;|m|在原点右侧,与m关于原点对称。
(2) -n < m < |m| < n。
答案:
例2:
(1) -n在原点左侧,与n关于原点对称;|m|在原点右侧,与m关于原点对称。
(2) -n < m < |m| < n。
变式训练:D
(1) -n在原点左侧,与n关于原点对称;|m|在原点右侧,与m关于原点对称。
(2) -n < m < |m| < n。
变式训练:D
查看更多完整答案,请扫码查看


