第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 在$0$,$-\frac{2}{3}$,$1$,$-3$四个数中,最小的数是(
A.$0$
B.$-\frac{2}{3}$
C.$1$
D.$-3$
D
)A.$0$
B.$-\frac{2}{3}$
C.$1$
D.$-3$
答案:
D
2. 在比较两个有理数的大小时,下列说法正确的是(
A.绝对值大的数一定大
B.绝对值大的数反而小
C.如果两个数中有负数,那么绝对值大的数反而小
D.在水平的数轴上,如果规定从原点向右为正方向,那么左边的数一定小于右边的数
D
)A.绝对值大的数一定大
B.绝对值大的数反而小
C.如果两个数中有负数,那么绝对值大的数反而小
D.在水平的数轴上,如果规定从原点向右为正方向,那么左边的数一定小于右边的数
答案:
D
3. 下列有理数的大小关系正确的是(
A.$-(-\frac{1}{3})<-|-\frac{1}{4}|$
B.$|+6|>|-6|$
C.$-|-3|>0$
D.$-\frac{3}{2}<-1.25$
D
)A.$-(-\frac{1}{3})<-|-\frac{1}{4}|$
B.$|+6|>|-6|$
C.$-|-3|>0$
D.$-\frac{3}{2}<-1.25$
答案:
D
4. 某天,有四个城市的平均气温分别是$0℃$,$10℃$,$-15℃$,$-1℃$,其中最低的气温是
$-15$
$℃$。
答案:
$-15$
5. 比较大小(填写“>”或“<”):
$-2$
$-2$
>
$-3$;$-\frac{10}{3}$<
$-\frac{22}{7}$;$-\frac{7}{8}$>
$-\frac{8}{9}$;$-(-\frac{3}{4})$<
$-[+(-\frac{4}{5})]$。
答案:
>;<;>;<
6. 有理数$a$,$b$在数轴上的对应点如图所示,下列结论中正确的是(
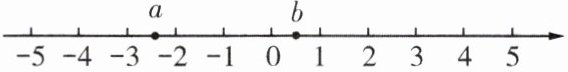
A.$a>-2$
B.$|a|>b$
C.$a>-b$
D.$|b|>|a|$
B
)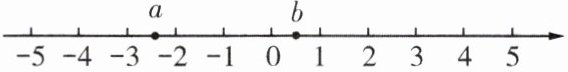
A.$a>-2$
B.$|a|>b$
C.$a>-b$
D.$|b|>|a|$
答案:
B
7. 已知有理数$a<0$,$b>0$,且$|a|<|b|$,把$a$,$-a$,$b$,$-b$按从小到大的顺序排列是
$-b \lt a \lt -a \lt b$
。
答案:
根据已知条件,$a$ 是负数,$b$ 是正数,且 $|a| \lt |b|$。
负数小于正数,所以 $a \lt b$ 和 $-b \lt -a$(因为$-a$是正数)。
由于$|a| \lt |b|$,则 $-b \lt a$ 的相反数是 $b \gt -a$,同时,由于 $a$ 是负数,其相反数 $-a$ 是正数,且 $-a \lt b$。
综合以上信息,可以得到:
$-b \lt a \lt -a \lt b$(因为$a$是负数,$b$是正数,且$|a| \lt |b|$,所以$-b$是最小的,$b$是最大的,而$a$比$-a$小)。
故答案为:$-b \lt a \lt -a \lt b$。
负数小于正数,所以 $a \lt b$ 和 $-b \lt -a$(因为$-a$是正数)。
由于$|a| \lt |b|$,则 $-b \lt a$ 的相反数是 $b \gt -a$,同时,由于 $a$ 是负数,其相反数 $-a$ 是正数,且 $-a \lt b$。
综合以上信息,可以得到:
$-b \lt a \lt -a \lt b$(因为$a$是负数,$b$是正数,且$|a| \lt |b|$,所以$-b$是最小的,$b$是最大的,而$a$比$-a$小)。
故答案为:$-b \lt a \lt -a \lt b$。
例1 将下列有理数填入适当的集合内:
$-2,5,-\frac{1}{2},\frac{2}{3},-0.05,4\frac{2}{3},0,-\vert -3\vert,8,(-\frac{1}{2})^{3}$。
正有理数集合:…$\{
整数集合:…$\{
负分数集合:…$\{
非负整数集合:…$\{
$-2,5,-\frac{1}{2},\frac{2}{3},-0.05,4\frac{2}{3},0,-\vert -3\vert,8,(-\frac{1}{2})^{3}$。
正有理数集合:…$\{
$5, \frac{2}{3}, 4\frac{2}{3}, 8$
\}$;整数集合:…$\{
$-2, 5, 0, -\vert -3\vert, 8$
\}$;负分数集合:…$\{
$-\frac{1}{2}, -0.05, (-\frac{1}{2})^{3}$
\}$;非负整数集合:…$\{
5, 0, 8
\}$。
答案:
正有理数集合:
$\{ 5, \frac{2}{3}, 4\frac{2}{3}, 8 \}$;
整数集合:
$\{ -2, 5, 0, -| -3 |, 8 \}$;
负分数集合:
$\{ -\frac{1}{2}, -0.05, (-\frac{1}{2})^{3} \}$;
非负整数集合:
$\{ 5, 0, 8 \}$。
$\{ 5, \frac{2}{3}, 4\frac{2}{3}, 8 \}$;
整数集合:
$\{ -2, 5, 0, -| -3 |, 8 \}$;
负分数集合:
$\{ -\frac{1}{2}, -0.05, (-\frac{1}{2})^{3} \}$;
非负整数集合:
$\{ 5, 0, 8 \}$。
巩固提升
(1)$\frac{3}{2}$的相反数是
(2)若$\vert 3x - 2\vert与(y - 3)^{2}$互为相反数,则$xy = $
(1)$\frac{3}{2}$的相反数是
$-\frac{3}{2}$
,$-5$的绝对值是$5$
。(2)若$\vert 3x - 2\vert与(y - 3)^{2}$互为相反数,则$xy = $
$2$
。
答案:
(1)$-\frac{3}{2}$,$5$;
(2)$2$
(1)$-\frac{3}{2}$,$5$;
(2)$2$
例2 画出数轴,在数轴上表示下列各数,并用“$<$”连接:
$+5,-3.5,\frac{1}{2},-1\frac{1}{2},4,0$。
$+5,-3.5,\frac{1}{2},-1\frac{1}{2},4,0$。
答案:
1. 画数轴(描述):
画一条水平直线,在直线上取一点作为原点$0$,规定直线上从原点向右为正方向,从原点向左为负方向,选取适当的单位长度(如$1$个单位长度),依次标出$+1,+2,+3,\cdots$和$-1,-2,-3,\cdots$等点。
2. 在数轴上表示各数:
$+5$在原点右边$5$个单位长度处;
$-3.5$在原点左边$3.5$个单位长度处;
$\frac{1}{2}$在原点右边$0.5$个单位长度处;
$-1\frac{1}{2}=-1.5$在原点左边$1.5$个单位长度处;
$4$在原点右边$4$个单位长度处;
$0$就在原点位置。
3. 用“$<$”连接各数:
$-3.5 < -1\frac{1}{2}<0<\frac{1}{2}<4 < +5$。
画一条水平直线,在直线上取一点作为原点$0$,规定直线上从原点向右为正方向,从原点向左为负方向,选取适当的单位长度(如$1$个单位长度),依次标出$+1,+2,+3,\cdots$和$-1,-2,-3,\cdots$等点。
2. 在数轴上表示各数:
$+5$在原点右边$5$个单位长度处;
$-3.5$在原点左边$3.5$个单位长度处;
$\frac{1}{2}$在原点右边$0.5$个单位长度处;
$-1\frac{1}{2}=-1.5$在原点左边$1.5$个单位长度处;
$4$在原点右边$4$个单位长度处;
$0$就在原点位置。
3. 用“$<$”连接各数:
$-3.5 < -1\frac{1}{2}<0<\frac{1}{2}<4 < +5$。
查看更多完整答案,请扫码查看


