第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
7. 对于一个正整数$m$,若将其各个数位上的数字两两作差后取绝对值,再从大到小顺次排列后,得到一个新数$n$,则称$n是m$的“绝对数”,例如:$m = 712$,将其各个数位上的数字两两作差后取绝对值为$6,5,1$,那么$m = 712$的“绝对数”$n为651$,按此定义,$645$的“绝对数”为
211
;若一个三位正整数$x$的“绝对数”为$431$,,则满足条件的所有$x$中最大的为985
.
答案:
211;985
填空 $(-3)×(-5)= $
$-4×\frac{1}{6}×(-3\frac{2}{5})= $
15
;$-4×\frac{1}{6}×(-3\frac{2}{5})= $
$\frac{34}{15}$
.
答案:
15;$\frac{34}{15}$
例1 计算:
(1)$0×\frac{1}{3}$; (2)$(-5)×12$;
(3)$(-2\frac{5}{12})×(-24)$.
名师导引 有理数乘法的运算顺序:先确定积的符号,再把因数的绝对值相乘.运算时,通常把带分数化为假分数,小数统一成分数.
(1)$0×\frac{1}{3}$; (2)$(-5)×12$;
(3)$(-2\frac{5}{12})×(-24)$.
名师导引 有理数乘法的运算顺序:先确定积的符号,再把因数的绝对值相乘.运算时,通常把带分数化为假分数,小数统一成分数.
答案:
(1) $0×\frac{1}{3}=0$
(2) $(-5)×12=-(5×12)=-60$
(3) $(-2\frac{5}{12})×(-24)$
$=(-\frac{29}{12})×(-24)$
$=\frac{29}{12}×24$
$=29×2$
$=58$
(1) $0×\frac{1}{3}=0$
(2) $(-5)×12=-(5×12)=-60$
(3) $(-2\frac{5}{12})×(-24)$
$=(-\frac{29}{12})×(-24)$
$=\frac{29}{12}×24$
$=29×2$
$=58$
变式训练 计算:
(1)$-3\frac{1}{4}×(-\frac{3}{13})=$
(2)$2\frac{4}{5}×2.5=$
(3)$(-0.7)×(-\frac{15}{4})=$
(4)$3\frac{1}{3}×0.3=$
(1)$-3\frac{1}{4}×(-\frac{3}{13})=$
$\frac{3}{4}$
;(2)$2\frac{4}{5}×2.5=$
$7$
;(3)$(-0.7)×(-\frac{15}{4})=$
$\frac{21}{8}$
;(4)$3\frac{1}{3}×0.3=$
$1$
.
答案:
(1)
首先将$-3\frac{1}{4}$转化为假分数$-\frac{13}{4}$,
则$-3\frac{1}{4}×(-\frac{3}{13})=-\frac{13}{4}×(-\frac{3}{13})=\frac{3}{4}$。
(2)
将$2\frac{4}{5}$转化为假分数$\frac{14}{5}$,$2.5=\frac{5}{2}$,
则$2\frac{4}{5}×2.5=\frac{14}{5}×\frac{5}{2}=7$。
(3)
将$-0.7$转化为分数$-\frac{7}{10}$,
则$(-0.7)×(-\frac{15}{4})=-\frac{7}{10}×(-\frac{15}{4})=\frac{21}{8}$。
(4)
将$3\frac{1}{3}$转化为假分数$\frac{10}{3}$,$0.3=\frac{3}{10}$,
则$3\frac{1}{3}×0.3=\frac{10}{3}×\frac{3}{10}=1$。
答案依次为:
(1)$\frac{3}{4}$;
(2)$7$;
(3)$\frac{21}{8}$;
(4)$1$。
(1)
首先将$-3\frac{1}{4}$转化为假分数$-\frac{13}{4}$,
则$-3\frac{1}{4}×(-\frac{3}{13})=-\frac{13}{4}×(-\frac{3}{13})=\frac{3}{4}$。
(2)
将$2\frac{4}{5}$转化为假分数$\frac{14}{5}$,$2.5=\frac{5}{2}$,
则$2\frac{4}{5}×2.5=\frac{14}{5}×\frac{5}{2}=7$。
(3)
将$-0.7$转化为分数$-\frac{7}{10}$,
则$(-0.7)×(-\frac{15}{4})=-\frac{7}{10}×(-\frac{15}{4})=\frac{21}{8}$。
(4)
将$3\frac{1}{3}$转化为假分数$\frac{10}{3}$,$0.3=\frac{3}{10}$,
则$3\frac{1}{3}×0.3=\frac{10}{3}×\frac{3}{10}=1$。
答案依次为:
(1)$\frac{3}{4}$;
(2)$7$;
(3)$\frac{21}{8}$;
(4)$1$。
例2 填空:
|原数|$-2$|
|倒数|
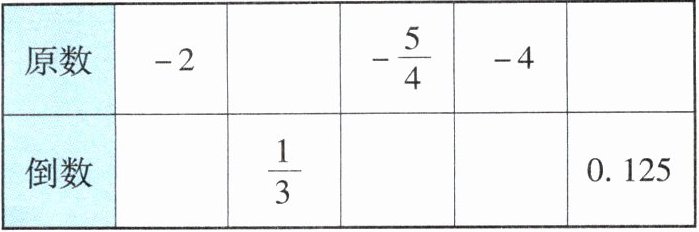
名师导引 (1)求小数的倒数,要先把小数化成分数;求带分数的倒数,要先把带分数化成假分数;(2)互为倒数的两个数的符号相同,记住这个结论可以避免发生符号错误;(3)0没有倒数;(4)倒数等于它本身的数有两个:$+1和-1$.
|原数|$-2$|
$3$
|$-\frac{5}{4}$|$-4$|$8$
||倒数|
$-\frac{1}{2}$
|$\frac{1}{3}$|$-\frac{4}{5}$
|$-\frac{1}{4}$
|$0.125$|
名师导引 (1)求小数的倒数,要先把小数化成分数;求带分数的倒数,要先把带分数化成假分数;(2)互为倒数的两个数的符号相同,记住这个结论可以避免发生符号错误;(3)0没有倒数;(4)倒数等于它本身的数有两个:$+1和-1$.
答案:
|原数|$-2$|$3$|$-\frac{5}{4}$|$-4$|$8$|
|倒数|$-\frac{1}{2}$|$\frac{1}{3}$|$-\frac{4}{5}$|$-\frac{1}{4}$|$0.125$|
|倒数|$-\frac{1}{2}$|$\frac{1}{3}$|$-\frac{4}{5}$|$-\frac{1}{4}$|$0.125$|
查看更多完整答案,请扫码查看


