《2025年学习指要七年级数学上册人教版》

巩固提升 某工程队要修路 $ a $ m,计划平均每天修 $ b $ m,则计划完成此项工程的时间为$\frac{a}{b}$天.

答案： $\frac{a}{b}$

例2 (1) 在 $ \pi,x^{2}+2,1 - 2x = 0,ab,a ＞ 3,0,\frac{a}{2} $ 中,代数式有(A)
A. $ 5 $ 个 B. $ 4 $ 个 C. $ 3 $ 个 D. $ 2 $ 个
(2) 学校买来 $ 20 $ 个足球,每个 $ a $ 元；又买来 $ b $ 个篮球,每个 $ 58 $ 元. $ 20a + 58b $ 表示买20个足球和b个篮球一共花的钱数；当 $ a = 45,b = 10 $ 时,$ 20a + 58b = $1480元.

答案： A；买20个足球和b个篮球一共花的钱数；1480

巩固提升 下列代数式的意义表述不正确的是(C)
A.$ (a + b)^{2} $ 表示 $ a $ 与 $ b $ 的和的平方
B.$ 8m $ 可表示 $ m $ 支单价为 $ 8 $ 元的钢笔的总价
C.$ \frac{3a}{2} + 4 $ 表示 $ a $ 的 $ 3 $ 倍与 $ 4 $ 的和的一半
D.$ 2a + b $ 表示 $ a $ 的 $ 2 $ 倍与 $ b $ 的和

答案： C

例3 已知 $ x^{2} - x - 1 = 0 $,则 $ x^{2} - x + 20 = $21.

答案： 21

巩固提升 若代数式 $ 3x - y $ 的值等于 $ 1 $,则代数式 $ 5 + 6x - 2y $ 的值是7.

答案： 7

1. 下列各式中,符合代数式书写规则的是(B)
A.$ 1\frac{1}{2}p $
B.$ 2y + x $
C.$ 2y ÷ x $
D.$ a × \frac{2}{3} $

答案： B

2. 下列说法中正确的个数是(B)
①正有理数和负有理数统称为有理数；②把 $ 3.14164 $ 精确到百分位,取得的近似数是 $ 3.14 $；③若三角形的面积一定,则它的底边长与底边上的高成反比例；④代数式 $ \frac{1}{a + b} $ 的意义是 $ a $ 与 $ b $ 的倒数的和.
A.$ 1 $
B.$ 2 $
C.$ 3 $
D.$ 4 $

答案： B

3. 下列图形都是由●按照一定规律组成的,其中第 $ 1 $ 个图中共有 $ 3 $ 个●,第 $ 2 $ 个图中共有 $ 7 $ 个●,第 $ 3 $ 个图中共有 $ 13 $ 个●,第 $ 4 $ 个图中共有 $ 21 $ 个●,……照此规律排列下去,则第 $ 7 $ 个图形中●的个数为(C)

A.$ 43 $
B.$ 47 $
C.$ 57 $
D.$ 61 $

答案： C

4. 当 $ a = 2,b = - 1,c = - 3 $ 时,求下列代数式的值：
(1) $ b^{2} - 4ac $； (2) $ a^{2} - 2ab + b^{2} $.

答案：
(1) 当 $a = 2$, $b = -1$, $c = -3$ 时，
$b^{2} - 4ac = (-1)^{2} - 4 × 2 × (-3) = 1 + 24 = 25$.
(2) 当 $a = 2$, $b = -1$ 时，
$a^{2} - 2ab + b^{2} = 2^{2} - 2 × 2 × (-1) + (-1)^{2} = 4 + 4 + 1 = 9$.

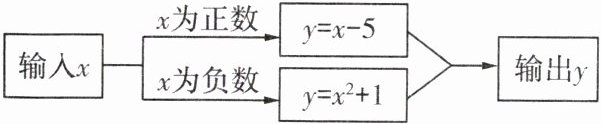
5. 根据如图的程序,如果输入 $ x = - 3 $,则输出的结果为10.

答案： $10$

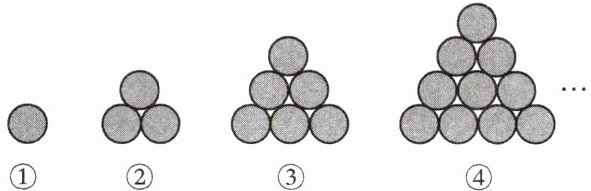
6. 按照下面的方式堆放小球,第 $ 1 $ 堆有 $ 1 $ 个小球,第 $ 2 $ 堆有 $ 3 $ 个小球,……则第 $ 5 $ 堆有15个小球,第 $ n $ 堆有$\frac{n(n+1)}{2}$个小球.

答案： 15；$\frac{n(n+1)}{2}$