《2025年同步练习西南大学出版社六年级数学上册西师大版重庆专版》

1. 你能证明“圆内接六边形的周长÷直径=3”吗？
（提示：先想一想三角形AOC是不是等边三角形。）

答案： 1. 圆内接正六边形的中心角为360°÷6=60°。
2. 连接圆心O与相邻两顶点（如A、B），OA=OB=半径r，∠AOB=60°，则△AOB为等边三角形，故边长AB=r。
3. 正六边形周长=6×边长=6r。
4. 圆的直径d=2r。
5. 周长÷直径=6r÷2r=3。
结论：圆内接六边形（正六边形）的周长÷直径=3。

2. 看下图，说一说刘徽割圆的过程。

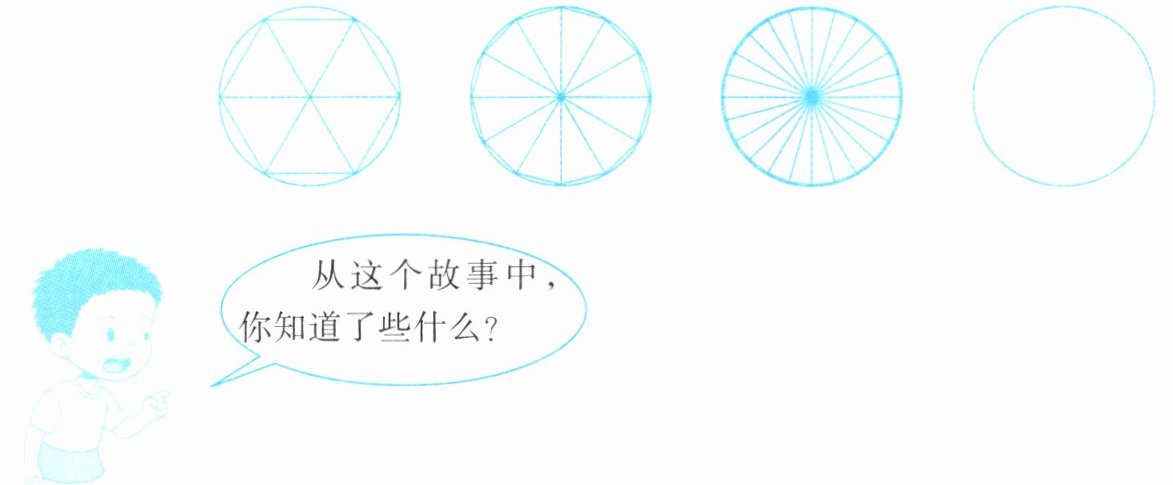
从这个故事中，你知道了些什么？

答案： 刘徽割圆的过程：首先从圆内接正六边形开始，将边数逐次加倍，得到正十二边形、正二十四边形、正四十八边形……随着边数的不断增加，正多边形的周长越来越接近圆的周长，面积也越来越接近圆的面积。
从这个故事中知道的：圆的面积可以通过不断增加圆内接正多边形的边数，用正多边形的面积近似代替圆的面积，边数越多，近似程度越高；体现了极限的数学思想。