《2025年新课程能力培养八年级数学上册人教版》

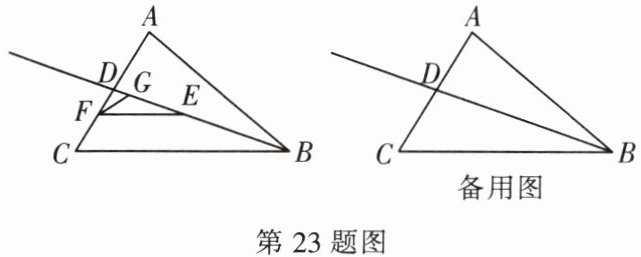
23. (12分)如图,在 $ \triangle ABC $ 中, $ BD $ 平分 $ \angle ABC $,交 $ AC $ 于点 $ D $,动点 $ E $ 在射线 $ BD $ 上(不与点 $ D $ 重合),过点 $ E $ 作 $ EF // BC $ 交线段 $ AC $ 于点 $ F $(不与点 $ A $, $ C $ 重合), $ \angle AFE $ 的平分线所在的直线与射线 $ BD $ 交于点 $ G $.
(1)当点 $ E $ 在线段 $ BD $ 上时,
①若 $ \angle ABC = 40° $, $ \angle C = 60° $, $ \angle FED $ 的度数为20°, $ \angle FGD $ 的度数为______50°；
②求证： $ \angle FGD = 90° - \frac{1}{2}\angle A $.
(2)当点 $ E $ 在线段 $ BD $ 的延长线上时,直接写出 $ \angle FGD $ 与 $ \angle A $ 之间的数量关系.∠FGD=$\frac{1}{2}$∠A

答案： 解：（1）①
∵∠ABC = 40°，∠C = 60°，
∴在△ABC中，∠A = 180° - ∠ABC - ∠C = 180° - 40° - 60° = 80°.
∵EF//BC，
∴∠FED = ∠CBD，∠DFE = ∠C = 60°.
∵BD平分∠ABC，FG平分∠AFE，
∴∠EBC = $\frac{1}{2}$∠ABC = 20°，∠GFE = $\frac{1}{2}$∠AFE = 30°，
∴∠FED = ∠EBC = 20°，∠FGD = ∠GFE + ∠FED = 30° + 20° = 50°.
②
∵BD平分∠ABC，
∴∠CBD = $\frac{1}{2}$∠ABC.
∵EF//BC，
∴∠FED = ∠CBD = $\frac{1}{2}$∠ABC，∠AFE = ∠ACB.
∵FG平分∠AFE，
∴∠EFG = $\frac{1}{2}$∠AFE = $\frac{1}{2}$∠ACB，
∴∠FGD = ∠EFG + ∠FED = $\frac{1}{2}$∠ACB + $\frac{1}{2}$∠ABC = $\frac{1}{2}$（180° - ∠A） = 90° - $\frac{1}{2}$∠A.
（2）∠FGD = $\frac{1}{2}$∠A.理由如下：如图，点E在线段BD的延长线上.
∵BD平分∠ABC，
∴∠CBD = $\frac{1}{2}$∠ABC.
∵EF//BC，
∴∠FED = ∠CBD = $\frac{1}{2}$∠ABC，∠EFC = ∠ACB，
∴∠AFE = 180° - ∠EFC = 180° - ∠ACB.
∵FH平分∠AFE，∠EFH = $\frac{1}{2}$∠AFE = 90° - $\frac{1}{2}$∠ACB，
∴∠FGD = ∠EFH - ∠FED = 90° - $\frac{1}{2}$∠ACB - $\frac{1}{2}$∠ABC = 90° - $\frac{1}{2}$（180° - ∠A） = $\frac{1}{2}$∠A.