17. (8分)先分解因式,再求值:$(4x + 5y)^2 - (3x - 2y)^2$,其中$x = \frac{1}{7}$,$y = 1$.
答案:
原式$=[(4x + 5y)+(3x - 2y)][(4x + 5y)-(3x - 2y)]=(4x + 5y + 3x - 2y)(4x + 5y - 3x + 2y)=(7x + 3y)(x + 7y)$,当$x = \frac{1}{7}$,$y = 1$时,原式$=(7×\frac{1}{7}+3×1)×(\frac{1}{7}+7×1)=\frac{200}{7}$.
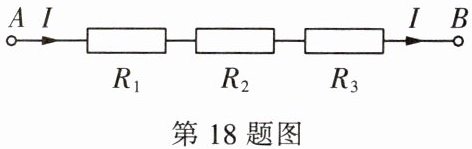
18. (7分)因式分解可以简化一些复杂的计算,如图,把$R_1$,$R_2$,$R_3$三个电阻串联起来,线路$AB$上的电流为$I$,电压为$U$,则$U = IR_1 + IR_2 + IR_3$.当$R_1 = 19.76\ \Omega$,$R_2 = 32.41\ \Omega$,$R_3 = 35.83\ \Omega$,$I = 2.5\ A$时,请利用因式分解计算出$U$的值.

答案:
$\because U = IR_{1}+IR_{2}+IR_{3}$,$R_{1}=19.76$,$R_{2}=32.41$,$R_{3}=35.83$,$I = 2.5$,$\therefore U = IR_{1}+IR_{2}+IR_{3}=I(R_{1}+R_{2}+R_{3})=2.5×(19.76 + 32.41 + 35.83)=2.5×88 = 220$.
19. (10分)阅读材料:要把多项式$am + an + bm + bn$分解因式,可以先把它进行分组再分解因式:$am + an + bm + bn = (am + an) + (bm + bn) = a(m + n) + b(m + n) = (m + n)(a + b)$,这种分解因式的方法叫作分组分解法.
(1)请用上述方法分解因式:$x^2 - y^2 + x - y$;
(2)已知$a - b = 3$,$a + c = -5$,求式子$ac - bc + a^2 - ab$的值.
(3)分解因式:$x^3 + 6x^2 + 11x + 6 =$
(1)请用上述方法分解因式:$x^2 - y^2 + x - y$;
(2)已知$a - b = 3$,$a + c = -5$,求式子$ac - bc + a^2 - ab$的值.
(3)分解因式:$x^3 + 6x^2 + 11x + 6 =$
$(x + 1)(x + 2)(x + 3)$
.
答案:
(1)原式$=(x + y)(x - y)+(x - y)=(x - y)(x + y + 1)$.
(2)$\because a - b = 3$,$a + c = - 5$,$\therefore$原式$=(ac + a^{2})-(bc + ab)=a(c + a)-b(c + a)=(c + a)(a - b)=-5×3 = - 15$.
(3)$(x + 1)(x + 2)(x + 3)$
(2)$\because a - b = 3$,$a + c = - 5$,$\therefore$原式$=(ac + a^{2})-(bc + ab)=a(c + a)-b(c + a)=(c + a)(a - b)=-5×3 = - 15$.
(3)$(x + 1)(x + 2)(x + 3)$
查看更多完整答案,请扫码查看


