《2025年新课程能力培养八年级数学上册人教版》

16. (8分) 如图，在 $ \triangle ABC $ 中，$ DE $ 是 $ AC $ 的中垂线，$ AE = 2\ cm $，$ \triangle ABD $ 的周长是 $ 10\ cm $，求 $ \triangle ABC $ 的周长.

答案： 解：
∵DE是AC的中垂线，
∴AE=CE=2，AD=DC.
∵△ABD的周长是10cm.
∴AB+BD+AD=10，
∴AB+BD+DC=AB+BC=10，
∴△ABC的周长是AB+BC+AC=10+2+2=14.

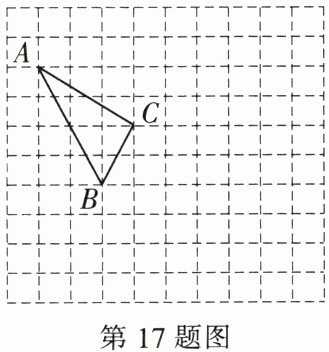
17. (8分) 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形 (顶点是网格线的交点的三角形) $ ABC $ 的顶点 $ A $，$ C $ 的坐标分别为 $ (-4,5) $，$ (-1,3) $.
(1) 请在如图所示的网格平面内作出平面直角坐标系.
(2) 请作出 $ \triangle ABC $ 关于 $ y $ 轴对称的 $ \triangle A'B'C' $.
(3) 写出点 $ B' $ 的坐标.
(4) 在 $ y $ 轴上找一点 $ P $，使得 $ PB = PC $.

答案：
解：（1）如图所示
（2）如图，△A'B'C'为所作.
（3）点B'的坐标为（2，1）.
（4）如图，点P为所作.

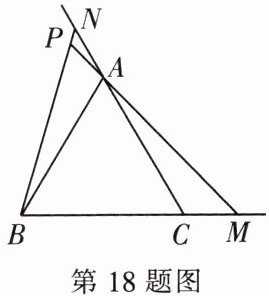
18. (8分) 如图，已知 $ \triangle ABC $ 为等边三角形，点 $ M $，$ N $ 分别在射线 $ BC $ 和射线 $ CA $ 上，且 $ BM = CN $，若 $ BN $ 与 $ MA $ 的延长线相交于点 $ P $，求 $ \angle BPM $ 的度数.

答案： 解：
∵△ABC是等边三角形，
∴AB=BC，∠ABM=∠BCN.在△BCN和△ABM中，$\left\{\begin{array}{l} BC=AB,\\ ∠BCN=∠ABM,\\ CN=BM,\end{array}\right. $
∴△BCN≌△ABM（SAS），
∴∠AMB=∠BNC.
∵△ABC是等边三角形，
∴∠ACB=60°，
∴∠AMB+∠CAM=∠ACB=60°.
∵∠AMB=∠BNC，∠CAM=∠NAP，
∴∠BNC+∠NAP=60°，
∴∠BPM=∠BNC+∠NAP=60°.