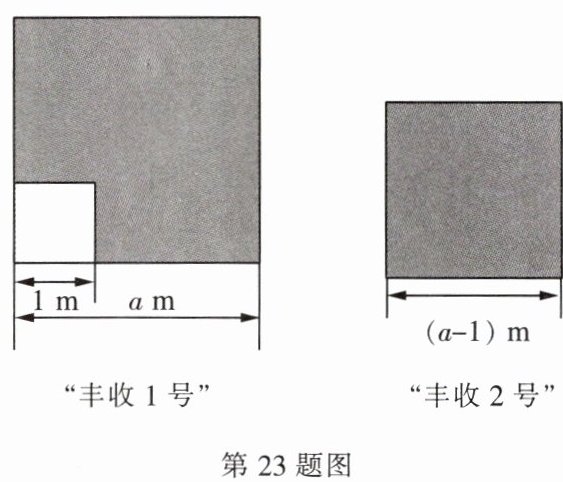
23. (12分)如图,“丰收1号”小麦试验田是边长为$am$($a>1$)的正方形去掉一个边长为1m的正方形蓄水池后余下的部分,“丰收2号”小麦试验田是边长为$(a - 1)m$的正方形,两块试验田的小麦都收获了500kg.
(1)①“丰收1号”单位面积产量为
②由图可知,
(2)若高的单位面积产量比低的单位面积产量多$\frac{40}{(a - 1)^{2}}kg/m^{2}$,求$a$的值.
(3)某农户试种“丰收1号”“丰收2号”两种小麦种子,两种小麦试种的单位面积产量与试验田一致,“丰收1号”小麦种植面积为$n m^{2}$($n$为整数),“丰收2号”小麦种植面积比“丰收1号”少55$m^{2}$.若两种小麦种植后,收获的产量相同,当$a<8且a$为整数时,符合条件的$n$的值为
(1)①“丰收1号”单位面积产量为
$\frac{500}{a^{2}-1}$
$kg/m^{2}$,“丰收2号”单位面积产量为$\frac{500}{(a-1)^{2}}$
$kg/m^{2}$;(以上结果均用含$a$的式子表示)②由图可知,
丰收2号
(填“丰收1号”或“丰收2号”)小麦的单位面积产量高.(2)若高的单位面积产量比低的单位面积产量多$\frac{40}{(a - 1)^{2}}kg/m^{2}$,求$a$的值.
解:根据题意,得$\frac{500}{(a-1)^{2}}-\frac{500}{a^{2}-1}=\frac{40}{(a-1)^{2}}$,解得$a=24$,经检验,当$a=24$时,$(a-1)^{2}(a+1)\neq 0$,∴$a=24$是原方程的解且符合题意.∴a的值是24.
(3)某农户试种“丰收1号”“丰收2号”两种小麦种子,两种小麦试种的单位面积产量与试验田一致,“丰收1号”小麦种植面积为$n m^{2}$($n$为整数),“丰收2号”小麦种植面积比“丰收1号”少55$m^{2}$.若两种小麦种植后,收获的产量相同,当$a<8且a$为整数时,符合条件的$n$的值为
110,165,220
.
答案:
解:(1)①由题意,“丰收1号”小麦的试验田的面积为$(a^{2}-1)\ m^{2}$,
∴“丰收1号”单位面积产量为$\frac{500}{a^{2}-1}\ kg$.由题意,“丰收2号”试验田的面积为$(a-1)^{2}\ m^{2}$,
∴“丰收2号”单位面积产量为$\frac{500}{(a-1)^{2}}\ kg$.故答案为$\frac{500}{a^{2}-1}$,$\frac{500}{(a-1)^{2}}$.②
∵$a>1$,
∴$a^{2}-1=(a+1)(a-1)>0$,$(a-1)^{2}>0$,
∴$a+1>a-1$,
∴$a^{2}-1>(a-1)^{2}$,
∴$\frac{500}{a^{2}-1}<\frac{500}{(a-1)^{2}}$,即“丰收2号”小麦的单位面积产量高.故答案为2号.(2)根据题意,得$\frac{500}{(a-1)^{2}}-\frac{500}{a^{2}-1}=\frac{40}{(a-1)^{2}}$,解得$a=24$,经检验,当$a=24$时,$(a-1)^{2}(a+1)\neq 0$,
∴$a=24$是原方程的解且符合题意.
∴a的值是24.(3)根据题意,得$\frac{500n}{a^{2}-1}=\frac{500(n-55)}{(a-1)^{2}}$,整理可得$a=\frac{2n-55}{55}$,
∴$n=\frac{55(a+1)}{2}$,当$a<8$时,$\frac{2n-55}{55}<8$,解得$n<\frac{495}{2}$,又
∵n为正整数,且满足$n=\frac{55(a+1)}{2}$,当$a=3$时,$n=\frac{55× 4}{2}=110$,当$a=5$时,$n=\frac{55× 6}{2}=165$,当$a=7$时,$n=\frac{55× 8}{2}=220$,
∴符合条件的n的值为110,165,220.故答案为110,165,220.
∴“丰收1号”单位面积产量为$\frac{500}{a^{2}-1}\ kg$.由题意,“丰收2号”试验田的面积为$(a-1)^{2}\ m^{2}$,
∴“丰收2号”单位面积产量为$\frac{500}{(a-1)^{2}}\ kg$.故答案为$\frac{500}{a^{2}-1}$,$\frac{500}{(a-1)^{2}}$.②
∵$a>1$,
∴$a^{2}-1=(a+1)(a-1)>0$,$(a-1)^{2}>0$,
∴$a+1>a-1$,
∴$a^{2}-1>(a-1)^{2}$,
∴$\frac{500}{a^{2}-1}<\frac{500}{(a-1)^{2}}$,即“丰收2号”小麦的单位面积产量高.故答案为2号.(2)根据题意,得$\frac{500}{(a-1)^{2}}-\frac{500}{a^{2}-1}=\frac{40}{(a-1)^{2}}$,解得$a=24$,经检验,当$a=24$时,$(a-1)^{2}(a+1)\neq 0$,
∴$a=24$是原方程的解且符合题意.
∴a的值是24.(3)根据题意,得$\frac{500n}{a^{2}-1}=\frac{500(n-55)}{(a-1)^{2}}$,整理可得$a=\frac{2n-55}{55}$,
∴$n=\frac{55(a+1)}{2}$,当$a<8$时,$\frac{2n-55}{55}<8$,解得$n<\frac{495}{2}$,又
∵n为正整数,且满足$n=\frac{55(a+1)}{2}$,当$a=3$时,$n=\frac{55× 4}{2}=110$,当$a=5$时,$n=\frac{55× 6}{2}=165$,当$a=7$时,$n=\frac{55× 8}{2}=220$,
∴符合条件的n的值为110,165,220.故答案为110,165,220.
查看更多完整答案,请扫码查看


