第45页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
变式2 下列是某科学研究小组探究杠杆平衡条件的实验过程(本实验均使用轻质杠杆)。
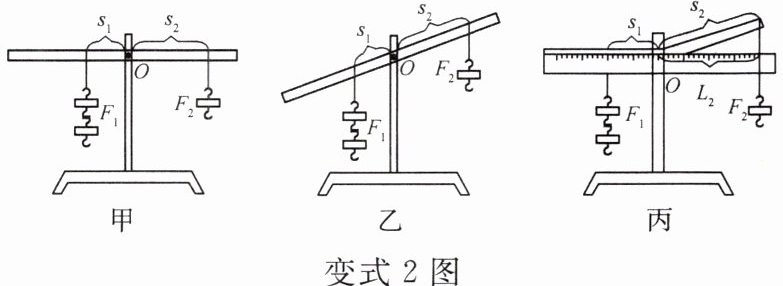
实验1:在直杠杆水平平衡时(如图甲所示)进行实验,记录多组数据得出:F₁×s₁=F₂×s₂(注:s₁和s₂分别表示支点O到F₁和F₂的作用点的距离)。在直杠杆倾斜平衡时(如图乙所示)进行实验,也得到了同样的结论。
该结论适用于所有平衡时的杠杆吗?
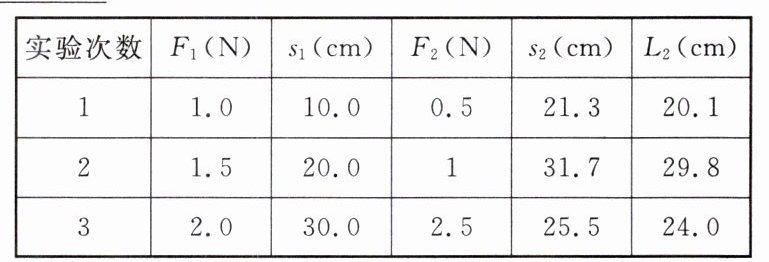
实验2:科学研究小组用一侧弯曲的杠杆进行如图丙所示的实验,移动钩码,改变钩码数量,记录数据如表所示,分析表格数据发现上述结论并不成立,但发现一个新的等量关系,即:▲。
s和L(支点到力的作用线的距离)这两个量在研究杠杆平衡条件时,哪个量才是有价值的呢?研究小组的同学观察到:支点到F₁的作用点的距离(s₁)与支点到F₁的作用线的距离(L₁)是相等的。研究小组的同学又进行了实验。
实验3:
①移动钩码,使弯杠杆▲并使弯杠杆处于平衡状态。
②记录F₁、s₁、L₁和F₂、s₂、L₂。
③改变钩码数量,移动钩码,记录弯杠杆处于平衡时的多组F₁、s₁、L₁和F₂、s₂、L₂。
④分析实验数据,得出弯杠杆的平衡条件。
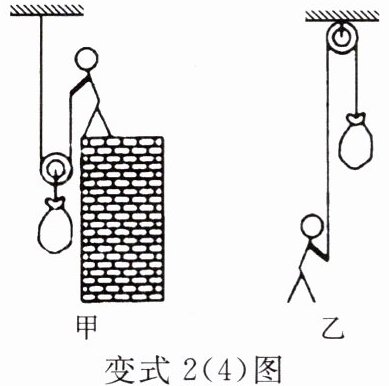
最后,通过科学思维,得出所有杠杆的平衡条件都是F₁×L₁=F₂×L₂。杠杆的平衡条件可用于解释许多杠杆应用,如用图甲方式提升物体比用图乙方式省力,就可用杠杆的平衡条件作出合理解释。
请回答下列问题:
(1)在实验2中研究一侧弯曲的杠杆时,发现的一个新的等量关系是
(2)将实验3中的①填写完整:______。
(3)“支点到力的作用线的距离”在科学上被称为
(4)用图甲方式提升物体比用图乙方式省力的原因是
实验1:在直杠杆水平平衡时(如图甲所示)进行实验,记录多组数据得出:F₁×s₁=F₂×s₂(注:s₁和s₂分别表示支点O到F₁和F₂的作用点的距离)。在直杠杆倾斜平衡时(如图乙所示)进行实验,也得到了同样的结论。

该结论适用于所有平衡时的杠杆吗?
实验2:科学研究小组用一侧弯曲的杠杆进行如图丙所示的实验,移动钩码,改变钩码数量,记录数据如表所示,分析表格数据发现上述结论并不成立,但发现一个新的等量关系,即:▲。

s和L(支点到力的作用线的距离)这两个量在研究杠杆平衡条件时,哪个量才是有价值的呢?研究小组的同学观察到:支点到F₁的作用点的距离(s₁)与支点到F₁的作用线的距离(L₁)是相等的。研究小组的同学又进行了实验。
实验3:
①移动钩码,使弯杠杆▲并使弯杠杆处于平衡状态。
②记录F₁、s₁、L₁和F₂、s₂、L₂。
③改变钩码数量,移动钩码,记录弯杠杆处于平衡时的多组F₁、s₁、L₁和F₂、s₂、L₂。
④分析实验数据,得出弯杠杆的平衡条件。
最后,通过科学思维,得出所有杠杆的平衡条件都是F₁×L₁=F₂×L₂。杠杆的平衡条件可用于解释许多杠杆应用,如用图甲方式提升物体比用图乙方式省力,就可用杠杆的平衡条件作出合理解释。

请回答下列问题:
(1)在实验2中研究一侧弯曲的杠杆时,发现的一个新的等量关系是
F₁×s₁=F₂×L₂
。(2)将实验3中的①填写完整:______。
(3)“支点到力的作用线的距离”在科学上被称为
力臂
,通过探究杠杆平衡条件的实验,使我们认识到建立这一科学量的价值。(4)用图甲方式提升物体比用图乙方式省力的原因是
图甲的动力臂大于阻力臂,图乙的动力臂等于阻力臂
。
答案:
(1)$F_{1}× s_{1}=F_{2}× L_{2}$
(2)倾斜或转动
(3)力臂
(4)图甲的动力臂大于阻力臂,图乙的动力臂等于阻力臂
(1)$F_{1}× s_{1}=F_{2}× L_{2}$
(2)倾斜或转动
(3)力臂
(4)图甲的动力臂大于阻力臂,图乙的动力臂等于阻力臂
典例3 为了将放置在水平地面上且重为84N的重物G提升到高处。小宁设计了如图甲所示的滑轮组装置。当小宁用如图乙所示随时间变化的竖直向下拉力F拉绳时,重物的速度v和上升的高度h随时间t变化的关系图像分别如图丙和丁所示。若重物与地面的接触面积S=5×10⁻²m²,不计摩擦和绳重。求:
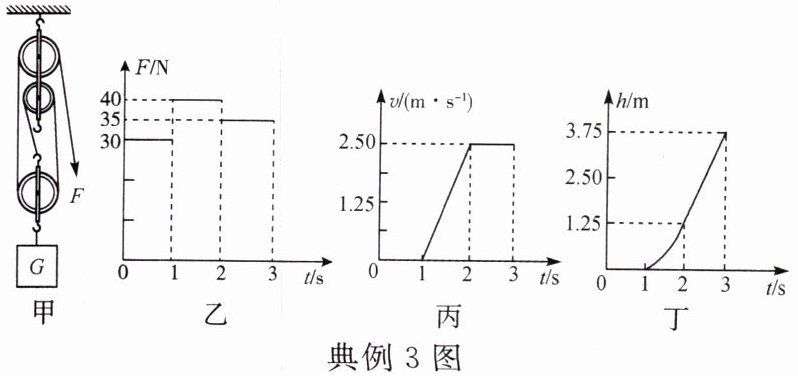
(1)在2~3s内,拉力F的功率P。
(2)动滑轮的重力。
(3)在1~2s内,拉力F做的功W。
(4)在0~1s内,重物对地面的压强p。

(1)在2~3s内,拉力F的功率P。
(2)动滑轮的重力。
(3)在1~2s内,拉力F做的功W。
(4)在0~1s内,重物对地面的压强p。
答案:
(1)2~3s内,拉力$F$的功率$P_{总}=Fv' = 35N×3×2.5m/s = 262.5W$。
在2~3s内,拉力$F$的功率为262.5W。
(2)在2~3s内,重物做匀速直线运动,根据$F=\frac{1}{3}(G + G_{动})$
得,动滑轮重$G_{动}=3F - G = 3×35N - 84N = 21N$。
动滑轮重21N。
(3)1~2s内,拉力做的功$W = Fs = Fnh = 40N×3×1.25m = 150J$。
在1~2s内,拉力$F$做功150J。
(4)在0~1s内,拉力$F = 30N$。
由$F=\frac{1}{3}(F_{拉}+G_{动})$得,在0~1s内,绳子对重物的拉力$F_{拉}=3F - G_{动}=3×30N - 21N = 69N$。
重物对地面的压力$F_{压}=G - F_{拉}=84N - 69N = 15N$。
重物对地面的压强$p=\frac{F_{压}}{S}=\frac{15N}{5×10^{-2}m^{2}} = 300Pa$。
在0~1s内,重物对地面的压强为300Pa。
(1)2~3s内,拉力$F$的功率$P_{总}=Fv' = 35N×3×2.5m/s = 262.5W$。
在2~3s内,拉力$F$的功率为262.5W。
(2)在2~3s内,重物做匀速直线运动,根据$F=\frac{1}{3}(G + G_{动})$
得,动滑轮重$G_{动}=3F - G = 3×35N - 84N = 21N$。
动滑轮重21N。
(3)1~2s内,拉力做的功$W = Fs = Fnh = 40N×3×1.25m = 150J$。
在1~2s内,拉力$F$做功150J。
(4)在0~1s内,拉力$F = 30N$。
由$F=\frac{1}{3}(F_{拉}+G_{动})$得,在0~1s内,绳子对重物的拉力$F_{拉}=3F - G_{动}=3×30N - 21N = 69N$。
重物对地面的压力$F_{压}=G - F_{拉}=84N - 69N = 15N$。
重物对地面的压强$p=\frac{F_{压}}{S}=\frac{15N}{5×10^{-2}m^{2}} = 300Pa$。
在0~1s内,重物对地面的压强为300Pa。
查看更多完整答案,请扫码查看


