第37页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
9. 一个物体由 $ A $ 点自由下落时,相继经过 $ B $、$ C $ 两点,如图所示,已知 $ AB = BC $,物体在 $ AB $ 段重力做功 $ W_{1} $,功率 $ P_{1} $;在 $ BC $ 段重力做功 $ W_{2} $,功率 $ P_{2} $,则下列关系正确的是(
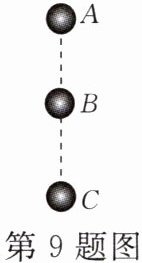
A.$ W_{1} = W_{2} $,$ P_{1} > P_{2} $
B.$ W_{1} = W_{2} $,$ P_{1} = P_{2} $
C.$ W_{1} = W_{2} $,$ P_{1} < P_{2} $
D.$ W_{1} < W_{2} $,$ P_{1} < P_{2} $
C
)
A.$ W_{1} = W_{2} $,$ P_{1} > P_{2} $
B.$ W_{1} = W_{2} $,$ P_{1} = P_{2} $
C.$ W_{1} = W_{2} $,$ P_{1} < P_{2} $
D.$ W_{1} < W_{2} $,$ P_{1} < P_{2} $
答案:
9.C
10. 2024 年 6 月 4 日,嫦娥六号上升器携带月球样品自月球背面起飞。
(1)若某次采集器将 $ 900 \, g $ 月壤从月球表面放入距月表 $ 1 \, m $ 高的收集器中,采集器克服月球重力做功为
(2)在返回过程中,若嫦娥六号上升器发动机以向上 $ 3000 \, N $ 的力工作 $ 6 \, min $,成功将携带样品的上升器送入到离月球表面高度约为 $ 15 \, km $ 的预定环月轨道。则嫦娥六号上升器发动机的功率至少为
(1)若某次采集器将 $ 900 \, g $ 月壤从月球表面放入距月表 $ 1 \, m $ 高的收集器中,采集器克服月球重力做功为
1.5 J
(已知物体在月球表面受到的重力是地球上的 $ \frac{1}{6} $,$ g_{地} $ 取 $ 10 \, N/kg $)。(2)在返回过程中,若嫦娥六号上升器发动机以向上 $ 3000 \, N $ 的力工作 $ 6 \, min $,成功将携带样品的上升器送入到离月球表面高度约为 $ 15 \, km $ 的预定环月轨道。则嫦娥六号上升器发动机的功率至少为
1.25×10^{5} W
。
答案:
$10.(1)1.5 J (2)1.25×10^{5} W$
11. 汽车行业经常用“马力”来描述车的动力性能。该词源自 18 世纪,瓦特利用一匹马匀速拉动 $ 4500 \, N $ 的重物(如图所示),该马在 $ 1 \, min $ 内将重物提升了约 $ 10 \, m $,瓦特便将这匹马在平均 $ 1 \, s $ 内所做的功称为 $ 1 $ 马力(不考虑绳重和摩擦)。
(1)该马在 $ 1 \, min $ 内做的功约为
(2)“马力”实际上是
(3)某电动汽车在 $ 150 $ 马力下,以 $ 90 \, km/h $ 的速度匀速通过一段 $ 15 \, km $ 长的平直桥面,该汽车在桥面上行驶过程中受到的阻力是多少?
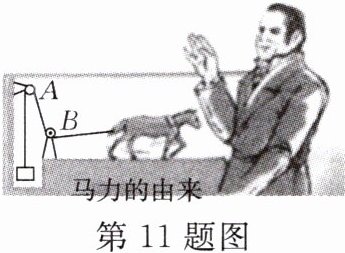
(1)该马在 $ 1 \, min $ 内做的功约为
45 000
$ J $。(2)“马力”实际上是
功率
(填量的名称)的单位。(3)某电动汽车在 $ 150 $ 马力下,以 $ 90 \, km/h $ 的速度匀速通过一段 $ 15 \, km $ 长的平直桥面,该汽车在桥面上行驶过程中受到的阻力是多少?

答案:
11.
(1)45 000
(2)功率
$(3)f=F=\frac{P}{v}=\frac{150×4500 N×\frac{10 m}{60 s}=4500 N}{\frac{90}{3.6}m/s}=4500 N。$
(1)45 000
(2)功率
$(3)f=F=\frac{P}{v}=\frac{150×4500 N×\frac{10 m}{60 s}=4500 N}{\frac{90}{3.6}m/s}=4500 N。$
12. 跳绳是一种简便易行的锻炼方式。如图所示是某同学某次跳绳时重心上升高度 $ h $ 随时间 $ t $ 变化的图像。该同学重心上升的最大高度为
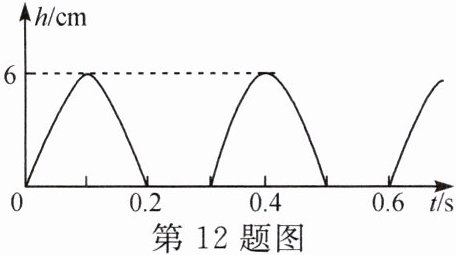
6
$ cm $。若该同学的体重为 $ 500 \, N $,则他 $ 1 \, min $ 内克服重力做功的平均功率为100
$ W $。
答案:
12.6 100
13. 某建筑工地用升降机提升大理石的示意图如图所示。货箱重为 $ 400 \, N $,$ g $ 取 $ 10 \, N/kg $。不计滑轮和钢丝绳的重力,不计摩擦。求:
(1)已知大理石的密度是 $ 2.8 × 10^{3} \, kg/m^{3} $,每块大理石的体积是 $ 1.0 × 10^{-2} \, m^{3} $,则每块大理石所受重力是多少?
(2)如果每段钢丝绳上能承受的最大拉力是 $ 2000 \, N $,则该升降机一次最多能匀速提升多少块大理石?
(3)某次提升中,升降机在 $ 1 \, min $ 内将货物匀速提升了 $ 15 \, m $,施加在钢丝绳上的拉力 $ F $ 是 $ 2000 \, N $。则钢丝绳上拉力 $ F $ 的功率是多少?
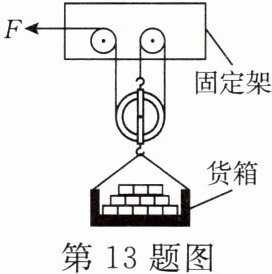
(1)已知大理石的密度是 $ 2.8 × 10^{3} \, kg/m^{3} $,每块大理石的体积是 $ 1.0 × 10^{-2} \, m^{3} $,则每块大理石所受重力是多少?
(2)如果每段钢丝绳上能承受的最大拉力是 $ 2000 \, N $,则该升降机一次最多能匀速提升多少块大理石?
(3)某次提升中,升降机在 $ 1 \, min $ 内将货物匀速提升了 $ 15 \, m $,施加在钢丝绳上的拉力 $ F $ 是 $ 2000 \, N $。则钢丝绳上拉力 $ F $ 的功率是多少?

答案:
13.
(1)根据$\rho=\frac{m}{V}$可得,每块大理石的质量$m=\rho V=2.8×10^{3} kg/m^{3}×1.0×10^{-2} m^{3}=28 kg,$每块大理石所受重力G=mg=28 kg×10 N/kg=280 N。
每块大理石所受重力是280 N。
(2)该升降机一次能够提起的总重$G_{总}=3×F_{max}=3×2000 N=6000 N,$则该升降机一次能提升的大理石的总重$G_{石}=G_{总}-G_{箱}=6000 N-400 N=5600 N,$升降机一次最多能提升的大理石的块数$n=\frac{G_{石}}{G}=\frac{5600 N}{280 N}=20$块。
该升降机一次最多能匀速提升20块大理石。
(3)钢丝绳左端移动的距离s=3h=3×15 m=45 m,把货物提升15 m拉力F做的功$W=Fs=2000 N×45 m=9×10^{4} J,$则钢丝绳上拉力F的功率$P=\frac{W}{t}=\frac{9×10^{4} J}{60 s}=1500 W。$
钢丝绳上拉力F的功率是1500 W。
(1)根据$\rho=\frac{m}{V}$可得,每块大理石的质量$m=\rho V=2.8×10^{3} kg/m^{3}×1.0×10^{-2} m^{3}=28 kg,$每块大理石所受重力G=mg=28 kg×10 N/kg=280 N。
每块大理石所受重力是280 N。
(2)该升降机一次能够提起的总重$G_{总}=3×F_{max}=3×2000 N=6000 N,$则该升降机一次能提升的大理石的总重$G_{石}=G_{总}-G_{箱}=6000 N-400 N=5600 N,$升降机一次最多能提升的大理石的块数$n=\frac{G_{石}}{G}=\frac{5600 N}{280 N}=20$块。
该升降机一次最多能匀速提升20块大理石。
(3)钢丝绳左端移动的距离s=3h=3×15 m=45 m,把货物提升15 m拉力F做的功$W=Fs=2000 N×45 m=9×10^{4} J,$则钢丝绳上拉力F的功率$P=\frac{W}{t}=\frac{9×10^{4} J}{60 s}=1500 W。$
钢丝绳上拉力F的功率是1500 W。
查看更多完整答案,请扫码查看


