2025年智趣暑假作业云南科技出版社八年级数学华师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年智趣暑假作业云南科技出版社八年级数学华师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图所示,在菱形 $ABCD$ 中,$\angle BAD = 80^{\circ}$,$AB$ 的垂直平分线交对角线 $AC$ 于点 $F$,垂足为 $E$,连接 $DF$,则 $\angle CDF$ 等于 (
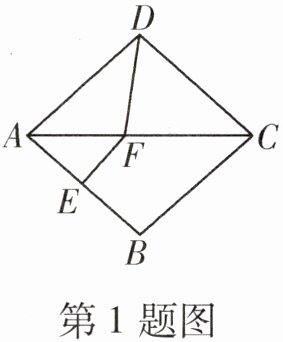
A.$50^{\circ}$
B.$60^{\circ}$
C.$70^{\circ}$
D.$80^{\circ}$
B
)
A.$50^{\circ}$
B.$60^{\circ}$
C.$70^{\circ}$
D.$80^{\circ}$
答案:
B
2. 菱形 $OABC$ 在平面直角坐标系中的位置如图所示,若 $OA = 2$,$\angle AOC = 45^{\circ}$,则 $B$ 点的坐标是 (
A.$(2 + \sqrt{2}, \sqrt{2})$
B.$(-2 - \sqrt{2}, -\sqrt{2})$
C.$(2 - \sqrt{2}, \sqrt{2})$
D.$(-2 - \sqrt{2}, \sqrt{2})$
D
)A.$(2 + \sqrt{2}, \sqrt{2})$
B.$(-2 - \sqrt{2}, -\sqrt{2})$
C.$(2 - \sqrt{2}, \sqrt{2})$
D.$(-2 - \sqrt{2}, \sqrt{2})$
答案:
D
3. 如图所示,在 $□ ABCD$ 中,$AE$,$CF$ 分别是 $\angle BAD$ 和 $\angle BCD$ 的平分线. 添加一个条件,仍无法判断四边形 $AECF$ 为菱形的是 (
A.$AE = AF$
B.$EF \perp AC$
C.$\angle ABC = 60^{\circ}$
D.$AC$ 是 $\angle EAF$ 的平分线
C
)A.$AE = AF$
B.$EF \perp AC$
C.$\angle ABC = 60^{\circ}$
D.$AC$ 是 $\angle EAF$ 的平分线
答案:
C
1. 如图所示,菱形 $ABCD$ 的边长为 $2$,且 $AE \perp BC$ 于点 $E$,$AF \perp CD$ 于点 $F$,$\angle B = 60^{\circ}$,则菱形的面积为______
$ 2 \sqrt { 3 } $
.
答案:
$ 2 \sqrt { 3 } $
2. 如图,已知菱形 $ABCD$ 的两条对角线分别为 $6$ 和 $8$,$M$,$N$ 分别是边 $BC$,$CD$ 的中点,$P$ 是对角线 $BD$ 上一点,则 $PM + PN$ 的最小值为______
5
.
答案:
1. 首先,根据菱形的性质:
菱形的对角线互相垂直且平分,已知菱形$ABCD$的对角线$AC = 8$,$BD = 6$,设对角线$AC$与$BD$相交于点$O$,则$AO=\frac{1}{2}AC = 4$,$BO=\frac{1}{2}BD = 3$。
根据勾股定理$a^{2}+b^{2}=c^{2}$(这里$a = 3$,$b = 4$),可得边长$AB=\sqrt{AO^{2}+BO^{2}}=\sqrt{4^{2}+3^{2}} = 5$。
2. 然后,作$M$关于$BD$的对称点$Q$:
因为菱形的性质,点$M$关于$BD$的对称点$Q$在$AB$上,且$BQ = BM$。
又因为$M$,$N$分别是$BC$,$CD$的中点,所以$BQ=\frac{1}{2}BC$,$DN=\frac{1}{2}CD$,而$BC = CD$,所以$BQ = DN$,且$BQ// DN$,则四边形$BQND$是平行四边形。
所以$QN = BD$(这里利用平行四边形对边相等),连接$NQ$,$NQ$与$BD$的交点即为$P$(此时$PM + PN$最小,根据两点之间线段最短)。
实际上,我们可以利用平移和对称的性质,$PM + PN$的最小值等于$AC$的一半与$BD$的一半构成的直角三角形的斜边(另一种方法:连接$AC$,$CM$,$CN$,根据中位线定理和对称性质)。
取$AC$的中点$E$,连接$ME$,$NE$($ME// AB$,$NE// AD$),$M$关于$BD$的对称点$Q$,$PM = PQ$,$PM + PN=PQ + PN$。
当$Q$,$P$,$N$共线时,$PM + PN$最小,此时$PM + PN$的值等于$5$(根据菱形的性质和中位线定理:
连接$AM$,$AN$,$AC$,$BD$相交于$O$,$M$关于$BD$的对称点$A$(因为菱形对角线平分一组对角,$BD$是角平分线,$AB = BC$,$M$是$BC$中点,所以$A$,$M$关于$BD$对称)。
连接$AN$,$AN$与$BD$的交点$P$,此时$PM + PN=PA + PN$。
根据三角形中位线定理,$M$,$N$是中点,$AB = CD = 5$(由勾股定理$AB=\sqrt{(\frac{6}{2})^{2}+(\frac{8}{2})^{2}} = 5$),$AN$是$\triangle ACD$的中位线,$AM$是$\triangle ABC$的中位线,$PM + PN$的最小值为$5$($AN=\frac{1}{2}AC$,$AM=\frac{1}{2}AB$,利用平行四边形$AMCN$($AM// CN$,$AM = CN$),$PM + PN$的最小值等于菱形的边长)。
所以$PM + PN$的最小值为$5$。
菱形的对角线互相垂直且平分,已知菱形$ABCD$的对角线$AC = 8$,$BD = 6$,设对角线$AC$与$BD$相交于点$O$,则$AO=\frac{1}{2}AC = 4$,$BO=\frac{1}{2}BD = 3$。
根据勾股定理$a^{2}+b^{2}=c^{2}$(这里$a = 3$,$b = 4$),可得边长$AB=\sqrt{AO^{2}+BO^{2}}=\sqrt{4^{2}+3^{2}} = 5$。
2. 然后,作$M$关于$BD$的对称点$Q$:
因为菱形的性质,点$M$关于$BD$的对称点$Q$在$AB$上,且$BQ = BM$。
又因为$M$,$N$分别是$BC$,$CD$的中点,所以$BQ=\frac{1}{2}BC$,$DN=\frac{1}{2}CD$,而$BC = CD$,所以$BQ = DN$,且$BQ// DN$,则四边形$BQND$是平行四边形。
所以$QN = BD$(这里利用平行四边形对边相等),连接$NQ$,$NQ$与$BD$的交点即为$P$(此时$PM + PN$最小,根据两点之间线段最短)。
实际上,我们可以利用平移和对称的性质,$PM + PN$的最小值等于$AC$的一半与$BD$的一半构成的直角三角形的斜边(另一种方法:连接$AC$,$CM$,$CN$,根据中位线定理和对称性质)。
取$AC$的中点$E$,连接$ME$,$NE$($ME// AB$,$NE// AD$),$M$关于$BD$的对称点$Q$,$PM = PQ$,$PM + PN=PQ + PN$。
当$Q$,$P$,$N$共线时,$PM + PN$最小,此时$PM + PN$的值等于$5$(根据菱形的性质和中位线定理:
连接$AM$,$AN$,$AC$,$BD$相交于$O$,$M$关于$BD$的对称点$A$(因为菱形对角线平分一组对角,$BD$是角平分线,$AB = BC$,$M$是$BC$中点,所以$A$,$M$关于$BD$对称)。
连接$AN$,$AN$与$BD$的交点$P$,此时$PM + PN=PA + PN$。
根据三角形中位线定理,$M$,$N$是中点,$AB = CD = 5$(由勾股定理$AB=\sqrt{(\frac{6}{2})^{2}+(\frac{8}{2})^{2}} = 5$),$AN$是$\triangle ACD$的中位线,$AM$是$\triangle ABC$的中位线,$PM + PN$的最小值为$5$($AN=\frac{1}{2}AC$,$AM=\frac{1}{2}AB$,利用平行四边形$AMCN$($AM// CN$,$AM = CN$),$PM + PN$的最小值等于菱形的边长)。
所以$PM + PN$的最小值为$5$。
查看更多完整答案,请扫码查看


