《2025年智趣暑假作业云南科技出版社八年级数学华师大版》

2. 如图,平行四边形ABCD的对角线相交于点O,且$AB\neq AD$,过点O作$OE\perp BD$交BC于点E. 若$\triangle CDE$的周长为10,则平行四边形ABCD的周长为20.

答案： 20

3. 如图所示,已知$□ ABCD$的对角线交于点O,过点O作直线分别交AB,CD的反向延长线于点E,F,且$OE= 6$,则$OF= $6.

答案： 6

1. 如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连接AD,AC,CE,使$AB= AC$.
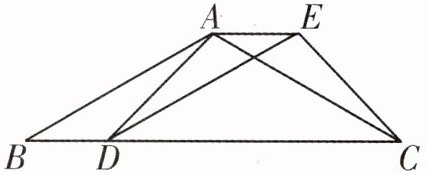
(1)求证：$\triangle BAD\cong \triangle ACE$；
(2)若$\angle B= 30^{\circ}$,$\angle ADC= 45^{\circ}$,$BD= 10$,求平行四边形ABDE的面积.

答案： 1. （1）
证明：
因为四边形$ABDE$是平行四边形，所以$AE// BD$，$AE = BD$，$AB = DE$，$\angle B+\angle BAE = 180^{\circ}$。
又因为$AB = AC$，所以$AC = DE$，$\angle B=\angle ACB$。
由$AE// BD$可得$\angle CAE=\angle ACB$，所以$\angle B=\angle CAE$。
在$\triangle BAD$和$\triangle ACE$中，$\begin{cases}AB = AC\\\angle B=\angle CAE\\BD = AE\end{cases}$。
根据$SAS$（边角边）定理，可得$\triangle BAD\cong\triangle ACE$。
2. （2）
解：
过点$A$作$AG\perp BC$于点$G$。
设$AG = x$。
在$Rt\triangle AGD$中，$\angle ADC = 45^{\circ}$，$\tan\angle ADC=\frac{AG}{DG}$，因为$\tan45^{\circ}=1$，所以$DG = AG=x$。
在$Rt\triangle ABG$中，$\angle B = 30^{\circ}$，$\tan\angle B=\frac{AG}{BG}$，$\tan30^{\circ}=\frac{\sqrt{3}}{3}$，则$BG=\sqrt{3}x$。
因为$BD = BG - DG$，$BD = 10$，所以$\sqrt{3}x−x = 10$，即$x(\sqrt{3}-1)=10$，解得$x = 5(\sqrt{3}+1)$。
因为$AE = BD = 10$（平行四边形对边相等）。
根据平行四边形面积公式$S = BD× AG$。
把$BD = 10$，$AG = 5(\sqrt{3}+1)$代入可得$S=10×5(\sqrt{3}+1)=50\sqrt{3}+50$。
综上，（1）已证$\triangle BAD\cong\triangle ACE$；（2）平行四边形$ABDE$的面积为$50 + 50\sqrt{3}$。

2. 如图,在平行四边形ABCD中,对角线AC,BD交于点O,经过点O的直线交AB于点E,交CD于点F.
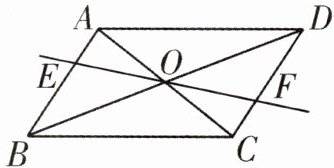
求证：$OE= OF$.

答案： $ \because $ 四边形 $ ABCD $ 是平行四边形，$ \therefore OA = OC $，$ AB // CD $，$ \therefore \angle OAE = \angle OCF $，又 $ \because \angle AOE = \angle COF $，$ \therefore \triangle OAE \cong \triangle OCF(ASA) $，$ \therefore OE = OF $