第69页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1.某校举办的“学党史知识竞赛”中共有 20 道题,每答对一题得 10 分,答错或不答都扣 5 分.墩墩同学想要得分超过 90 分,设他答对了 x 道题,则根据题意可列不等式为 ( )
A.$10x-5(20-x)\geqslant 90$
B.$10x-5(20-x)>90$
C.$10x-(20-x)\geqslant 90$
D.$10x-(20-x)>90$
A.$10x-5(20-x)\geqslant 90$
B.$10x-5(20-x)>90$
C.$10x-(20-x)\geqslant 90$
D.$10x-(20-x)>90$
答案:
B
2.一个工程队要在 6 天内完成$300m^{3}$的工程,已知第一天完成了$60m^{3}$,现在要比原计划至少提前 2 天完成,则以后几天平均每天至少要完成 ( )
A.$65m^{3}$
B.$70m^{3}$
C.$75m^{3}$
D.$80m^{3}$
A.$65m^{3}$
B.$70m^{3}$
C.$75m^{3}$
D.$80m^{3}$
答案:
D【解析】设以后几天平均每天要完成$x\ m^{3}$.由题意,得$60+(6-1-2)x \geqslant 300$,解得$x \geqslant 80$,$\therefore$以后几天平均每天至少要完成$80\ m^{3}$.
3.甲、乙两市出租车的收费标准如下表:
| | 起步价/元 | 3 km 后/(元/km) |
| 甲 | 10 | 2 |
| 乙 | 8 | 2.5 |
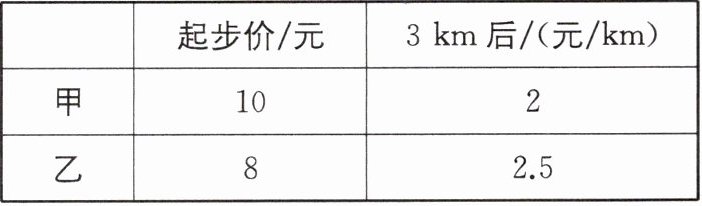
某人分别在两市乘坐出租车各行驶 x km(其中$x>3$),若在甲市的收费高于乙市,则 x 的取值范围为 ( )
A.$3\lt x<7$
B.$x>3$
C.$x>10$
D.$3\lt x<10$
| | 起步价/元 | 3 km 后/(元/km) |
| 甲 | 10 | 2 |
| 乙 | 8 | 2.5 |

某人分别在两市乘坐出租车各行驶 x km(其中$x>3$),若在甲市的收费高于乙市,则 x 的取值范围为 ( )
A.$3\lt x<7$
B.$x>3$
C.$x>10$
D.$3\lt x<10$
答案:
A【解析】$\because x > 3$,$\therefore$在甲市的收费为$10+2(x-3)=(2x+4)$元,在乙市的收费$8+2.5(x-3)=(2.5x+0.5)$元.由题意,得$2x+4 > 2.5x+0.5$,解得$x < 7$,$\therefore 3 < x < 7$.
4.为了加强学生的交通安全意识,某中学和交警大队联合举办了“我当一日小交警”活动,星期天选派部分学生到交通路口值勤,协助交通警察维护交通秩序.如果每个路口安排 4 人,那么还剩下 78 人;如果每个路口安排 8 人,那么最后一个路口不足 8 人,但不少于 4 人.该中学共选派值勤学生______人.
答案:
158【解析】设选派学生值勤的交通路口有$x$个,则该中学共选派值勤学生$(4x+78)$人.由题意,得$\begin{cases} 4x+78 \geqslant 8(x-1)+4,\\ 4x+78 < 8x,\\ \end{cases}$解得$\dfrac{39}{2} < x \leqslant \dfrac{41}{2}$.$\because x$为正整数,$\therefore x=20$,$\therefore 4x+78=4× 20+78=158$.
5.方方驾驶汽车匀速地从甲地开往乙地,设汽车的行驶速度为 v km/h,且全程速度不超过120 km/h.若她以 80 km/h 的速度行驶,则需6 h 到达乙地.如果方方想要在 5 h 内(包括5 h)到达乙地,那么 v 的取值范围是______.
答案:
$96 \leqslant v \leqslant 120$【解析】由题意,得$\begin{cases} 5v \geqslant 80× 6,\\ v \leqslant 120,\\ \end{cases}$解得$96 \leqslant v \leqslant 120$.
6.用若干辆载质量为8t的汽车运载一批货物,若每辆汽车只装4t,则剩下20t货物;若每辆汽车装8t,则最后一辆汽车不满也不空.设用x辆汽车运载这批货物.
(1)这批货物共有______t(用含x的式子表示);
(2)求x的值.
(1)这批货物共有______t(用含x的式子表示);
(2)求x的值.
答案:
(1)$(4x+20)$
(2)由题意,得$0 < (4x+20)-8(x-1) < 8$,解得$5 < x < 7$.$\because x$为正整数,$\therefore x=6$.
(1)$(4x+20)$
(2)由题意,得$0 < (4x+20)-8(x-1) < 8$,解得$5 < x < 7$.$\because x$为正整数,$\therefore x=6$.
7.在一条笔直的公路上有相距 30 km 的 A,B 两地,甲骑自行车以 15 km/h 的速度从 A 地到 B地,同时乙骑自行车以 30 km/h 的速度从 B 地到 A 地.设骑行时间为 t h,试回答以下问题:
(1)求出甲、乙两人相遇时 t 的值;
(2)已知当两人之间的距离不超过 3 km 时,能够用无线对讲机联系,求出甲、乙两人能够用无线对讲机联系时 t 的取值范围.
(1)求出甲、乙两人相遇时 t 的值;
(2)已知当两人之间的距离不超过 3 km 时,能够用无线对讲机联系,求出甲、乙两人能够用无线对讲机联系时 t 的取值范围.
答案:
(1)由题意,得$15t+30t=30$,解得$t=\dfrac{2}{3}$.
(2)相遇前两人之间的距离是$[30-(15+30)t]\ km$,相遇后两人之间的距离是$[(15+30)t-30]\ km$.由题意,得$\begin{cases} 30-(15+30)t \leqslant 3,\\ (15+30)t-30 \leqslant 3,\\ \end{cases}$解得$\dfrac{3}{5} \leqslant t \leqslant \dfrac{11}{15}$.答:甲、乙两人能够用无线对讲机联系时$t$的取值范围是$\dfrac{3}{5} \leqslant t \leqslant \dfrac{11}{15}$.
(1)由题意,得$15t+30t=30$,解得$t=\dfrac{2}{3}$.
(2)相遇前两人之间的距离是$[30-(15+30)t]\ km$,相遇后两人之间的距离是$[(15+30)t-30]\ km$.由题意,得$\begin{cases} 30-(15+30)t \leqslant 3,\\ (15+30)t-30 \leqslant 3,\\ \end{cases}$解得$\dfrac{3}{5} \leqslant t \leqslant \dfrac{11}{15}$.答:甲、乙两人能够用无线对讲机联系时$t$的取值范围是$\dfrac{3}{5} \leqslant t \leqslant \dfrac{11}{15}$.
查看更多完整答案,请扫码查看


